Основи z-перетворення та його властивості.

Основи z - перетворення. Дискретну функцію f [nT₀] можна аналітично записати у вигляді ряду:

(3.12)

де f(t) – породжувальна безперервна функція; d(t-nT₀) – зміщена на час nT₀ дельта-функція.

Перетворення Лапласа від функції (3.12) має вигляд:

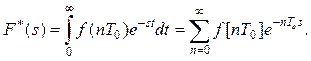(3.13)

Це перетворення називається дискретним перетворенням Лапласа. У символічній формі його записують так:

Якщо аргументом безперервної функції є відносний час t/T₀, то формула дискретного перетворення матиме вигляд:

(3.14)

де q=sT₀ – комплексне число, яке називається параметром дискретного перетворення Лапласа.

Зображення F^*(s) і F^*(q) є трансцендентними функціями від s і q, що робить неможливим застосування звичайних методів аналізу в площині s або q для дослідження імпульсних систем. Більш прийнятним є z - перетворення. Формула z–перетворення випливає з формули (3.14), якщо виконати підстановку e^q = z. Вона має вигляд:

(3.15)

Розглянемо основні властивості z-перетворення стосовно незміщених решітчастих функцій.

1. Властивість лінійності. Зображення лінійної комбінації решітчастих функцій дорівнює такій самій лінійній комбінації їх зображень.

2. Запізнювання і випередження (зсув за часом на ціле число періодів). Для решітчастої функції, зсунутої вправо (запізнюючої) на m періодів, маємо:

Z{f [n-m]}= z^-mF(z), (3.16)

де F(z) – зображення функції f [n].

Для решітчастої функції, зсунутої вліво (випереджуючої) на m періодів, маємо:

Z{f [n + m]}= (3.17)

3. Множення оригіналу на експоненту Зображення незміщеної решітчастої функції записуємо у вигляді:

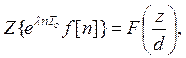
(3.18)

4. Зображення різниць (аналог зображення похідної). Для різниці k-го порядку за нульових початкових умов, тобто n=0, маємо:

Z{D^k f [n]} = (z-1)^k F(z), (3.19)

звідки для першої різниці (k=1)

Z{D f [n]} = (z-1) F(z).

5. Зображення суми (аналог зображення інтеграла). Зображення суми має вигляд:

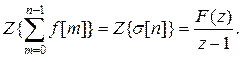(3.20)

6. Початкове значення решітчастої функції. При n=0 значення решітчастої функції обчислюється за формулою:

(3.21)

7. Кінцеве значення решітчастої функції. При n = ¥ запишемо:

(3.22)

8. Згортка решітчастих функцій. Якщо

Z{f₁[n]} = F₁(z) і Z{f₂[n]} = F₂(z),

то

F₁(z)F₂(z) = (3.23)

9. Зображення функції 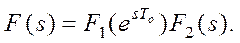Маємо

Z{F(s)} = F₁(z) Z{F₂(s)}.

Дата добавления: 2015-10-29