
|
Читайте также: |
Ізокліною називається геометричне місце точок фазової площини, в яких фазові траєкторії мають однаковий нахил, тобто лінія, яку всі фазові траекторії перетинають під одним кутом. Із геометричного змісту похідної (тангенс кута нахилу дотичної до графіка функції) та диференціального рівняння фазових траекторій можна записати:
 , /*/
, /*/
де  - нахил фазової траекторії на фазовій площині.
- нахил фазової траекторії на фазовій площині.
Отже у кожній точці фазової площини можна знайти цілком визначену величину нахилу фазової траекторії.
Спосіб побудови полягає у наступному. Із рівняння /*/ знаходимо функцію
 , /**/
, /**/
яка являє собою рівняння ізоклін.
Побудуємо ряд ізоклін 1-4 за рівнянням (**). У точці  ізокліни 1 (рис. 1.6) проведемо дві прямі
ізокліни 1 (рис. 1.6) проведемо дві прямі  і
і  з нахилами
з нахилами 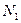 і
і  відповідно до перетину з ізокліною 2. Отриманий на ній відрізок
відповідно до перетину з ізокліною 2. Отриманий на ній відрізок  поділимо навпіл і через точку
поділимо навпіл і через точку  проведемо дві прямі
проведемо дві прямі  і
і  з нахилами
з нахилами  і
і  до перетину з ізокліною 3. Потім відрізок
до перетину з ізокліною 3. Потім відрізок  поділимо навпіл точкою
поділимо навпіл точкою 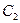 , через яку проводимо прямі
, через яку проводимо прямі  і
і 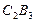 з нахилами
з нахилами  і
і  і т.д. Через знайдені точки
і т.д. Через знайдені точки  ,
, 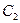 ,
,  , …,
, …,  проводимо фазову траєкторію. Точність побудови фазової траєкторії за методом ізоклін буде тим вища, чим частіше на графіку нанесені ізокліни.
проводимо фазову траєкторію. Точність побудови фазової траєкторії за методом ізоклін буде тим вища, чим частіше на графіку нанесені ізокліни.

Рис. 1.6 - Побудова фазової траєкторії за методом ізоклін
Метод комп’ютерного моделювання:

4. Види з’єднань нелінійних елементів та розрахунок сумарних характеристик.

Якщо у систему входить декілька нелінійних елементів, з’єднаних послідовно, паралельно або зустрічно-паралельно, то сумарну характеристику можна побудувати за певними правилами. Паралельне з’єднання нелінійних елементів. При паралельному з’єднанні нелінійних елементів сумарну характеристику будують як геометричну суму нелінійних характеристик окремих елементів (рис. 1.1).
 |
 і
і 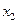 .У першій чверті будують характеристику НЕ1, в другій – НЕ2, в третій проводять бісектрису, за допомогою якої у четвертій чверті отримують сумарну нелінійну характеристику (рис. 1.2 б).
.У першій чверті будують характеристику НЕ1, в другій – НЕ2, в третій проводять бісектрису, за допомогою якої у четвертій чверті отримують сумарну нелінійну характеристику (рис. 1.2 б).З’єднання нелінійних елементів зі зворотнім зв’язком. Рис. 1.3. а) структурна схема з’єднання елементів зі зворотнім звязком; б) побудова сумарної (ІІІ) нелінійної характеристики; в) побудова сумарної (ІІІ) нелінійної характеристики при додатньому зворотньому звязку

При побудові результуючої характеристики нелінійного елемента НЕ1, охопленого нелінійним зворотнім зв’язком з характеристикою НЕ2 (рис. 1.3 а) в першому квадранті будуємо характеристику елемента НЕ1, а в другому – елемента НЕ2, повернувши систему координат протигодинникової стрілки на 90 градусів (щоб вісь вихідного сигналу НЕ1 співпала з віссю вхідного сигналу НЕ2). В цьому випадку результуюча характеристика отримається як геометрична сума характеристик НЕ1 та НЕ2, просумованих в напрямку осі хвх.
5. Розрізняють такі типи імпульсної модуляції (рис.3.2):
Амплітудно - імпульсну модуляцію (AІМ), при якій змінюється амплітуда 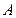 вихідних імпульсів у залежності від значень вхідної величини в моменти квантування
вихідних імпульсів у залежності від значень вхідної величини в моменти квантування  , де
, де  - коефіцієнт передачі імпульсного елемента.
- коефіцієнт передачі імпульсного елемента.
Широтно-імпульсну модуляцію (ШІМ), при якій змінюється ширина імпульсів  в залежності від значень вхідної величини в моменти квантування. Величину
в залежності від значень вхідної величини в моменти квантування. Величину  - називають відносною тривалістю імпульсів. Вона показує яку частину періоду слідування імпульсів складає його тривалість.
- називають відносною тривалістю імпульсів. Вона показує яку частину періоду слідування імпульсів складає його тривалість.
Фазово–імпульсну модуляцію (ФІМ), при якій відбувається часовий зсув імпульсів  у залежності від значень вхідної величини в моменти квантування.
у залежності від значень вхідної величини в моменти квантування.
З усіх видів імпульсної модуляції найпростішою є АІМ. У випадку АІМ імпульсний елемент є лінійною динамічною ланкою.При амплітудно-імпульсній модуляції імпульсний елемент виробляє прямокутні імпульси однакової тривалості з амплітудою, пропорційною величині вхідного сигналу в моменти квантування. 
З усіх видів імпульсної модуляції найпростішою є АІМ. У випадку АІМ імпульсний елемент є лінійною динамічною ланкою.При амплітудно-імпульсній модуляції імпульсний елемент виробляє прямокутні імпульси однакової тривалості з амплітудою, пропорційною величині вхідного сигналу в моменти квантування.
Широке застосування систем керування з різними видами модуляції сигналу пояснюється низкою їх переваг:
- можливість багатоканального керування, тобто дискретний керуючий пристрій можна використовувати для одночасного керування декількома однотипними об’єктами;
- можливість стикування з цифровими обчислювальними пристроями, що дозволяє реалізувати більш складні закони керування;
- можливість тривалого збереження і запам’ятовування інформації;
- висока завадостійкість, надійність; підвищена точність передавання і перетворення сигналів;
- менші габарити та вага; зручність для агрегатного-блочної побудови систем.
САК з імпульсною модуляцією сигналу відрізняється від безперервної системи наявністю імпульсного модулятора, який перетворює безперервний вхідний сигнал на послідовність імпульсів. Залежно від того, який з параметрів імпульсної послідовності модулюється, тобто змінюється під дією модулюючого сигналу, розрізняють:
- амплітудно-імпульсний модулятор, якщо модулюється амплітуда вихідних імпульсів; при цьому тривалість імпульсів t= const і період слідування  ;
;
- широтно-імпульсний модулятор, якщо модулюється ширина (тривалість) t вихідних імпульсів; при цьому амплітуда  ;
;  ;
;
- частотно-імпульсний модулятор, якщо модулюється частота повтору імпульсів у вихідній імпульсній послідовності; амплітуда і тривалість імпульсів постійні, тобто  ; t = const.
; t = const.
6. Випадкові процеси в автоматичних системах керування
При попередніх розрахунках ми припускали, що зовнішні впливи (керуючі дії та збурення), є визначеними відомими функціями часу. У цих випадках стан системи, що описується звичайними диференціальними рівняннями, у будь-який момент часу t однозначно визначається станом системи у попередній момент часу t0 < t. Звичайно вибирають t0 = 0 і кажуть, що стан системи однозначно визначається початковими умовами і може бути точно передбаченим для будь-якого моменту часу t. Такі системи називаються детермінованими.
Однак на практиці часто зустрічаються впливи, закон зміни яких має випадковий характер і не може бути наперед точно визначений. Такими випадковими впливами є, наприклад, добові зміни навантаження енергосистеми; пориви вітру, що діють на літак; удари хвиль у гідродинамічних системах; флуктуаційні шуми у радіотехнічних пристроях тощо. При випадкових впливах даних про стан системи у момент t0 недостатньо, щоб судити про її стан у подальший момент часу t > t0.
Випадкові дії можуть прикладатися до системи зовні (зовнішні дії) або виникати усередині деяких її елементів (внутрішні шуми). Випадкові зміни властивостей системи звичайно можна звести до еквівалентного впливу деяких випадкових завад, що діють на неї, тому далі будемо вважати, що на систему діють тільки зовнішні випадкові впливи.
Розрахунок систем автоматичного керування при випадкових діях виконують за допомогою спеціальних статистичних методів. САУ, що спроектована на основі цих методів, буде забезпечувати виконання вимог, до цієї системи не тільки для одного детермінованого впливу, а для цілої сукупності впливів, що задані за допомогою статистичних характеристик.
Статистичні методи дозволяють з’ясувати лише закономірності, що є притаманними випадковим явищам масового характеру. Наприклад, якщо помилка системи має випадковий характер, то точне її значення у будь-який момент часу за допомогою статистичного розрахунку передбачити неможливо. Однак, якщо провести багато вимірювань помилки у однакових умовах, то, наприклад, середнє значення помилки можна шляхом статистичного розрахунку передбачити з достатньою точністю.
7. Випадкові процеси та їх основні статистичні характеристики
Функція, значення якої при кожному значенні незалежної змінної є випадковою величиною, називається випадковою функцією. Випадкові функції, для яких змінною є час t, називають випадковими процесами або стохастичними процесами.
Статистичні властивості випадкової величини х визначають за її функцією розподілу (інтегральним законом розподілу) F(x) або за щільністю ймовірності (диференціальним законом розподілу) w(x).
Випадкові величини можуть мати різні закони розподілу: рівномірний, нормальний, експоненціальний тощо. У багатьох задачах автоматичного керування дуже часто використовують нормальний закон розподілу (закон Гауса), який має місце, якщо випадкова величина визначається сумарним ефектом від впливу великої кількості різних незалежних факторів.
З курсу теорії ймовірності відомо, що випадкова величина х при нормальному законі розподілу повністю визначається математичним сподіванням (середнім значенням) mx і середнім квадратичним відхиленням sх.
Математичним сподіванням (середнім значенням) mx(t) випадкового процесу X(t) називають величину:
 (2.9)
(2.9)
де w1(x, t) – одномірна щільність ймовірності випадкового процесу X(t).
Математичне сподівання випадкового процесу X(t) являє собою деяку невипадкову (регулярну) функцію часу mx(t), біля якої групуються і відносно якої коливаються усі реалізації даного випадкового процесу. Математичне сподівання називають середнім значенням випадкового процесу за множиною (статистичним середнім), оскільки воно являє собою ймовірносно усереднене значення нескінченної множини реалізацій випадкового процесу.
Середнім значенням квадрата випадкового процесу називають величину:
 (2.10)
(2.10)
Часто розглядають так званий центрований випадковий процес 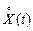 - відхилення випадкового процесу X(t) від його середнього значення mx(t):
- відхилення випадкового процесу X(t) від його середнього значення mx(t):
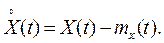
Іноді зручно використовувати статистичні характеристики випадкового процесу, які мають ту саму розмірність, що й сама випадкова величина:
- середнє квадратичне значення випадкового процесу:
 (2.16)
(2.16)
що дорівнює арифметичному значенню квадратного кореня із середнього значення квадрата випадкового процесу;
- середнє квадратичне відхилення випадкового процесу:
 (2.17)
(2.17)
що дорівнює арифметичному значенню квадратного кореня із дисперсії випадкового процесу.
8. Система управління називається дискретною, якщо вона містить хоча б один дискретний елемент. Елемент називається дискретним, якщо його вихідний сигнал квантується по часу або по рівню. Кажуть, що сигнал квантований по часу, якщо він являє собою послідовність імпульсів, і квантованим по рівню, якщо він приймає дискретні значення, тобто значення, кратні певній мінімальній величині, яку називають рівнем квантування, або квантом.
Розрізняють три види квантування сигналів: за рівнем, за часом, за рівнем і за часом одночасно.
Квантування за рівнем полягає у фіксації визначених дискретних значень безперервного сигналу. При цьому безперервний сигнал замінюється сигналом, який змінюється східчасто. Суміжні дискретні значення відрізняються одне від одного на постійну величину  , яка називається кроком квантування. Перехід з одного рівня на інший відбувається у моменти часу, коли безперервний сигнал досягає чергового фіксованого значення (рис. 3.1, а), або коли сигнал проходить середину інтервалу між двома суміжними значеннями (рис. 3.1, б).
, яка називається кроком квантування. Перехід з одного рівня на інший відбувається у моменти часу, коли безперервний сигнал досягає чергового фіксованого значення (рис. 3.1, а), або коли сигнал проходить середину інтервалу між двома суміжними значеннями (рис. 3.1, б).
Квантування за часом полягає у фіксації значень безперервного сигналу в рівновіддалені один від одного дискретні моменти часу. При цьому квантований сигнал може мати східчасту форму (рис. 3.1, в) або являти собою послідовність імпульсів (рис. 3.1, г). Суміжні моменти відрізняються один від одного на постійну величину Dt = T, яка називається інтервалом дискретності або періодом повтору.
Під час сумісного квантування за рівнем і за часом фіксуються дискретні за рівнем значення, найближчі до значень безперервного сигналу в дискретні моменти часу (рис. 3.1, д, е).
Залежно від виду квантування, що застосовується, всі дискретні системи можна розділити на три класи:
- релейні; у них квантування відбувається за рівнем;
- імпульсні, в яких квантування відбувається за часом;
- цифрові (релейно-імпульсні) з квантуванням і за рівнем, і за часом.

9. Метод ізоклін.
Ізокліною називається геометричне місце точок фазової площини, в яких фазові траєкторії мають однаковий нахил, тобто лінія, яку всі фазові траекторії перетинають під одним кутом. Із геометричного змісту похідної (тангенс кута нахилу дотичної до графіка функції) та диференціального рівняння фазових траекторій можна записати:
 , /*/
, /*/
де  - нахил фазової траекторії на фазовій площині.
- нахил фазової траекторії на фазовій площині.
Отже у кожній точці фазової площини можна знайти цілком визначену величину нахилу фазової траекторії.
Спосіб побудови полягає у наступному. Із рівняння /*/ знаходимо функцію
 , /**/
, /**/
яка являє собою рівняння ізоклін.
Побудуємо ряд ізоклін 1-4 за рівнянням (**). У точці  ізокліни 1 (рис. 1.6) проведемо дві прямі
ізокліни 1 (рис. 1.6) проведемо дві прямі  і
і  з нахилами
з нахилами  і
і  відповідно до перетину з ізокліною 2. Отриманий на ній відрізок
відповідно до перетину з ізокліною 2. Отриманий на ній відрізок  поділимо навпіл і через точку
поділимо навпіл і через точку  проведемо дві прямі
проведемо дві прямі  і
і  з нахилами
з нахилами  і
і  до перетину з ізокліною 3. Потім відрізок
до перетину з ізокліною 3. Потім відрізок  поділимо навпіл точкою
поділимо навпіл точкою 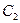 , через яку проводимо прямі
, через яку проводимо прямі  і
і 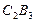 з нахилами
з нахилами  і
і  і т.д. Через знайдені точки
і т.д. Через знайдені точки  ,
, 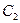 ,
,  , …,
, …,  проводимо фазову траєкторію. Точність побудови фазової траєкторії за методом ізоклін буде тим вища, чим частіше на графіку нанесені ізокліни.
проводимо фазову траєкторію. Точність побудови фазової траєкторії за методом ізоклін буде тим вища, чим частіше на графіку нанесені ізокліни.
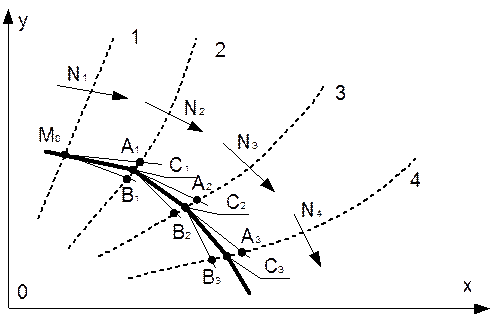
Рис. 1.6 - Побудова фазової траєкторії за методом ізоклін
Дата добавления: 2015-10-29; просмотров: 263 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Методи розрахунку та побудови фазових портретів | | | Дослідження параметрів автоколивань методом гармонічного балансу |