Дослідження параметрів автоколивань методом гармонічного балансу

При використанні методу гармонічної лінеаризації приймається, що гіпотеза фільтра виконується. Тоді, в системі виникає періодичний процес і на виході лінійної частини і на вході нелінійної ланки він є гармонічним . Тому періодичний режим однозначно визначається частотою 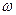та амплітудою 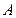, і дослідження періодичного процесу зводиться до визначення цих параметрів.

Основна умова виникнення періодичного процесу. В лінеаризованій системі можуть виникати гармонічні коливання, якщо її характеристичне рівняння має чисто уявні корені, або, якщо амплітудно-фазова характеристика розімкнутої системи проходить через точку 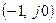, тобто якщо виконується рівність

. (-+)

Це співвідношення є рівнянням відносно невідомих параметрів, частоти 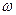та амплітуди 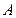і визначає основну умову виникнення періодичних процесів у системі що розглядається. Автоколивання в системі можливі якщо дане рівняння має дійсні додатні корені.

Є кілька методів дослідження автоколивань. Першим розглянемо аналітичний метод.

Підставивши в рівняння (-+) вирази для передаточних функцій лінійної та лінеаризованої частин, та позбувшись дробу, отримаємо рівняння у вигляді

,

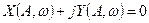або

(--++)

Якщо остання система рівнянь має розв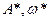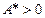’язок (, ), то це означає, що гармонічно лінеаризоване рівняння має розв’язок яке описує періодичний процес.

Розв’язок описує автоколивання, якщо він асимптотично орбітально стійкий. Таким чином, дослідження автоколивань зводиться до розв’язку рівнянь (--++) та визначення асимптотичної орбітальної стійкості.

У випадку коли нелінійна ланка має однозначну характеристику і її передаточна функція має вигляд , асимптотичну орбітальну стійкість можна перевірити, скориставшись умовою, що коефіцієнт гармонічної лінеаризації 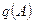повинен бути спадаючою функцією в околі точки , тобто повинна виконуватися нерівність

.

У випадку, коли нелінійна ланка має неоднозначну характеристику, для отримання умови асимптотичної орбітальної стійкості потрібно скористатися критерієм стійкості Михайлова. Основна умова виникнення періодичного процесу відповідає проходженню кривої Михайлова через початок координат. Умова асимптотичної орбітальної стійкості при неоднозначній характеристиці нелінійної ланки матиме вигляд

Зірочка при частинних похідних означає, що похідні визначаються в початку координат.

11. Дослідження стійкості нелінійних систем

Стійкість нелінійних систем є значно більш складним поняттям, ніж стійкість лінійних систем. Стійкість лінійних систем, для яких виправдовується принцип суперпозиції, є їх властивістю, тобто вимога стійкості до системи визначає структуру та значення її параметрів. При цьому фіксовані стани системи у визначені моменти часу і вхідні сигнали не мають ніякого значення. Лінійна система є або стійкою, або нестійкою і для дослідження стійкості існують порівняно прості математичні методи.

У зв’язку з тим, що у нелінійних системах може існувати особливий вид усталеного режиму – автоколивання, то необхідно дати коректне визначення стійкості. Таке визначення дав А.М.Ляпунов:

Незбурений рух стійкий, якщо при достатньо малих відхиленнях збурений рух наскільки завгодно мало відрізняється від незбуреного. При цьому система асимптотично стійка, якщо збурений рух прямує до незбуреного.

Для нелінійних систем розрізняють різні види стійкості в залежності від величини зовнішнього впливу:

- стійкість у "малому" – це стійкість системи при безмежно малих відхиленнях від усталеного режиму;

- стійкість у "великому" – стійкість при великих але обмежених відхиленнях (зовнішніх впливах) від усталеного режиму;

- стійкість у "цілому" – стійкість при будь-яких необмежених відхиленнях.

Стійкість називається асимптотичною, якщо система повертається до вихідного стану, тобто в ту саму точку з якої її вивів зовнішній вплив.

Стійкість називається неасимптотичною, якщо система повертається в деяку точку певному околі від вихідного режиму.

Абсолютна стійкість – стійкість цілого класу нелінійних систем, які мають таку нелінійність, яку можна вкласти в межі певного кута.

Перший непрямий метод дослідження стійкості Ляпунова. Використовується для дослідження стійкості в "малому". Він полягає в тому, що нелінійну систему лінеаризують, використовуючи розклад в ряд Тейлора. Тоді нелінійна система стійка, якщо лінеаризована система також стійка, і навпаки. Проте, якщо лінеаризована система виявиться на межі стійкості, то про стійкість нелінійної системи судити по ній не можна.

Для нелінійних систем вирішення питання стійкості є досить складним. Наприклад, рух або рівновага, стійкі у малому, можуть з’явитися нестійкими при великих відхиленнях. З іншого боку, при одних і тих самих вхідних сигналах система може мати декілька рівноважних станів. Тобто перший метод Ляпунова, що ґрунтується на дослідженні стійкості за рівняннями першого наближення, є недостатнім для повного дослідження стійкості нелінійних систем. Унаслідок цього для дослідження стійкості “у великому” і “у цілому” використовують спеціальні методи, до яких належать другий (прямий) метод Ляпунова та критерій стійкості Попова.

Другий (прямий) метод Ляпунова. Метод ґрунтується на побудові спеціальних функцій Ляпунова, які дозволяють отримати достатні умови стійкості рівноваги у великому. Дані функції V мають зміст відстані у спеціальному просторі станів між досліджуваним незбуреним і збуреним рухами. Якщо з часом ця функція спадає, тобто , то незбурений рух стійкий, а при 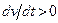- нестійкий.

Дослідження стійкості зводиться до аналізу швидкості зміни функції V. Умови стійкості сформульовані у двох теоремах Ляпунова.

Теорема 1. Якщо існує знаковизначена функція 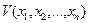, похідна якої за часом у силу диференціальних рівнянь руху є знакопостійною функцією протилежного з V знаку, або тотожно дорівнює нулю, то незбурений рух стійкий.

Теорема 2. Якщо, крім того, функція 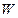знаковизначена, то незбурений рух стійкий асимптотично.

Відзначимо, що знакопостійною називається функція, яка набуває при всіх значеннях своїх аргументів тільки значення одного знаку або нульове значення. Знаковизначеною називається знакопостійна функція, яка набуває нульове значення тільки при нульовому значенні всіх її аргументів (на початку координат).

Складність даного методу полягає у тому, що задача вірного вибору функції Ляпунова пов’язана зі складнощами. Відсутні загальні методи побудови цих функцій. Більше того, зустрічаються випадки, коли система є стійкою, а внаслідок невірно вибраної функції Ляпунова цей факт установити не вдається. У такому випадку для розв’язання технічних задач метод Ляпунова не є досить ефективним.

12. Дослідження цифрових систем автоматичного управління

Квантування за часом робить ЦС дискретною, а квантування за рівнем – нелінійною. Однак при малому q (при великій роздільній здатності АЦП) впливом квантування за рівнем на динаміку системи можна знехтувати, тобто покласти q = 0. У цьому разі для дослідження ЦС можна застосовувати математичний апарат дослідження лінійних імпульсних систем з амплітудно-імпульсною модуляцією: дискретне z-перетворення і різницеві рівняння.

За умови врахування квантування сигналу і за часом і за рівнем цифрові системи слід віднести до класу нелінійних імпульсних систем і для їх дослідження застосовувати відповідні методи. Так, для дослідження абсолютної стійкості ЦС використовують критерій, розроблений Я.З.Ципкіним:

Положення рівноваги нелінійної імпульсної системи, приведена безперервна частина якої стійка, і нелінійна характеристика належить до сектору (0, k), буде абсолютно стійким, якщо для усіх частот у діапазоні (0, p) виконується нерівність:

(3.67)

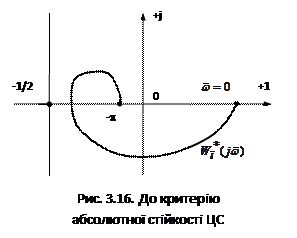
Геометрична інтерпретація даної нерівності дуже проста: амплітудно-фазова характеристика приведеної лінійної частини повинна розташовуватися праворуч від вертикальної лінії (–1/k).

Відповідно до рис. 3.14 для статичної характеристики АЦП k= q /(q /2)=2, тобто вона належить до сектора (0, 2). Тому умова абсолютної стійкості положення рівноваги ЦС виконується, якщо годограф розташований праворуч від вертикальної прямої (-1/2) (рис. 3.16).

У випадку, коли приведена лінійна частина нестійка, достатній критерій абсолютної стійкості (3.67) не виконується. Це пов’язано з тим, що характеристика АЦП має зону нечутливості (- q /2, + q /2), і коли процес потрапляє до цієї зони, система розмикається, а розімкнута система є нестійкою.

Якщо умова абсолютної стійкості не виконується, то у цифровій системі можуть виникати періодичні режими. Термін “автоколивання” у даному випадку не можна застосовувати, оскільки частота періодичних режимів визначається тактом роботи імпульсного елемента і, значить, ЦС не є автономною.

Дата добавления: 2015-10-29