Методи розрахунку та побудови фазових портретів

Аналітичне конструювання оптимальних регуляторів

Аналітичним конструюванням регуляторів (АКР) називається методика синтезу оптимального регулятора для заданого об’єкта при заданих обмеженнях і критерію оптимальності, що задається у квадратичній інтегральній формі вигляду (10.8):

.

Ця методика вперше була запропонована у роботах О.М.Льотова і Р.Калмана. Кожний з підходів має свої особливості, однак обидва рішення приводять до аналогічних результатів.

Суть задачі АКР полягає у визначенні варіаційними методами керуючої дії, яка мінімізує функціонал, що характеризує відхилення траєкторії справжнього руху системи від бажаної. У процесі аналітичного конструювання регуляторів відшукують закон керування у його аналітичній формі як деяку функцію фазових координат початкової системи. Таким чином, спочатку для заданого об’єкта керування при існуючих обмеженнях відшукують оптимальну траєкторію руху системи, а потім шляхом АКР визначають диференціальне рівняння (алгоритм керування) регулятора, що гарантує мінімальне відхилення траєкторії руху об’єкта керування від знайденої оптимальної траєкторії.

Узагалі рівняннями, що описують поведінку керуючого пристрою, можуть бути рівняння Ейлера, але вони не завжди виявляються такими, що реалізуються. Крім того, ці рівняння мають неприємну властивість: якщо час процесу керування у безперервній системі є скінченним, то рівняння Ейлера, що розглядають разом з рівняннями об’єкта, відповідають нестійкій системі регулювання. Так, у разі лінійного об’єкта і квадратичного функціоналу рівняння Ейлера є лінійними, причому серед коренів характеристичного рівняння обов’язково є як ліві, так і праві корені.

Якщо приєднання регулятора робить системи нестійкою, то це приєднання не може бути тривалим. Якщо відомо, що процес оптимального керування має спорадичний (одиничний, від випадку до випадку) характер, то можна піти на використання нестійкої системи, вмикаючи її лише на той момент, коли виникла потреба здійснити оптимальне керування, і обов’язково вимикаючи її після завершення керування. У тих випадках, коли регулятор має бути весь час підключеним до об’єкта, необхідно вжити заходів щодо забезпечення стійкості системи.

Цю задачу можна розв’язати шляхом відкидання у розв’язку рівняння складових, що відповідають додатним кореням. При цьому час керування стає нескінченно великим, проте функціонал набуває найменше з усіх можливих значення для різних Т.

Методи розрахунку та побудови фазових портретів

До основних методів розрахунку та побудови фазових портретів відносять: аналітичні; графічний наближений (метод ізоклін) та методи побудови за допомогою компьютерного моделювання.

Аналітичний метод.

Даний метод базується на розвязуванні диференціальних рівнянь руху системи.

Для початку необхідно отримати дифереціальні рівняння фазових траекторій, для чого нелінійне диференціальне рівняння системи другого порядку необхідно привести до нормальної форми Коші. Для цього спочатку диференціальне рівняння динаміки системи розв’язується відносно старшої похідної. Результат такого розв’язку можна записати у вигляді:

- загальний вигляд нелінійного диференціального рівняння, розв’язаного відносно старшої похідної,

де - регульована величина; 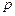- нелінійна функція.Наприклад, маємо нелінійне рівняння другого порядку Розв’язавши його відносно старшої похідної отримаємо .Для переходу до нормальної форми Коші здійснюємо підстановку

і отримаємо диференціальне рівняння системи у формі Коші:

Для отримання диференціального рівняння фазових траекторій, необхідно з диференціальних рівнянь у формі Коші виключити час. Цього можна досягти, поділивши перше диференціальне рівняння на друге. Отримаємо:

- диференціальне рівняння фазових траекторій.

Для побудови фазового портрету розв’язуємо диференціальне рівняння траекторій (розділяємо змінні та інтегруємо). Після чого проводимо побудову.

Дата добавления: 2015-10-29