Метод гармонічної лінеаризації

Метод гармонічної лінеаризації, або метод гармонічного балансу першочергово було розроблено для дослідження періодичних режимів. Однак з часом він став використовуватися для аналізу стійкості та синтезу нелінійних систем.

Основна ідея методу полягає в наступному. Керовані системи (об’єкти), як правило, мають властивості фільтра низьких частот: при виникненні періодичних режимів вони не пропускають або пропускають зі значним ослабленням другі та більш високі гармоніки. І суть методу гармонічної лінеаризації полягає в описі нелінійної ланки лінійним рівнянням, яке отримується при нехтуванні (відкиданні) вказаними гармоніками в розкладі нелінійної функції в ряд Фур’є.

Метод гармонічної лінеаризації є наближеним методом. Однак його перевагою є те, що його можна застосовувати до систем будь-якого порядку, на відміну від методу фазової площини.

Структурну схему замкнутої нелінійної системи, яка складається з нелінійної ланки та лінійної частини – лінійної ланки, будемо називати типовою структурною схемою нелінійної системи (рис.1.7).

Рис1.7. Типова структурна схема нелінійної САУ

Приймемо, що задаючий вплив . Рівняння системи мають вигляд:

, , . (+*)

Припустимо, що в системі виникає періодичний режим. Тоді нелінійна функція буде періодичною функцією часу, і її можна буде розкласти в ряд Фур’є:

,

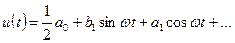де 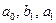- коефіцієнти Фур’є; ; - період; трьома крапками позначені вищі (другі та більш високі) гармоніки.

Припустимо, що лінійна частина має властивості фільта низьких частот, тобто виконується умова

, ,

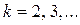
За цієї умови вищі гармоніки не здійснюють суттєвого впливу на вихідну величину лінійної частини. Тому при визначенні вищими гармоніками можна знехтувати, і рівняння системи (+*) представити у вигляді

, , . (+*+)

Якщо в системі виникає періодичний режим і лінійна частина є фільтром низьких частот, тобто справедлива гіпотеза фільтра, то коливання на виході лінійної частини і відповідно на вході нелінійної ланки є гармонічними.

Виберемо початок відліку так, щоб на вході нелінійної ланки 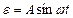. Тоді маємо

, .

Підставивши ці вирази в (+*+), при отримаємо

, , , (+**+)

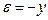де

, ,

або, якщо - однозначна нечітка функція, ,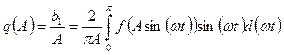

Система (+**+) при фіксованих амплітуді та частоті є лінійною. Перехід від вихідної системи (+*) до лінеаризованої системи (+**+) називається гармонічною лінеаризацією. Коефіцієнти та називають коефіцієнтами гармонічної лінеаризації. Передаточну функцію

називають передаточною функцією нелінійної ланки і відповідно вираз ,

який отримується при підстановці в передаточну функцію нелінійної ланки , називають частотною передаточною функцією нелінійної ланки. В останньому виразі коефіцієнти та являють собою дійсну та уявну частини. Тому будемо називати дійсним, а - уявним коефіцієнтом гармонічної лінеаризації.

Розрахунок коефіцієнтів гармонічної лінеаризації базується на побудові графіка вихідного сигналу нелінійної ланки, коли на її вхід подається гармонічний сигнал .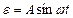

25. Перший непрямий метод дослідження стійкості Ляпунова. Використовується для дослідження стійкості в "малому". Він полягає в тому, що нелінійну систему лінеаризують, використовуючи розклад в ряд Тейлора. Тоді нелінійна система стійка, якщо лінеаризована система також стійка, і навпаки. Проте, якщо лінеаризована система виявиться на межі стійкості, то про стійкість нелінійної системи судити по ній не можна.

Для нелінійних систем вирішення питання стійкості є досить складним. Наприклад, рух або рівновага, стійкі у малому, можуть з’явитися нестійкими при великих відхиленнях. З іншого боку, при одних і тих самих вхідних сигналах система може мати декілька рівноважних станів. Тобто перший метод Ляпунова, що ґрунтується на дослідженні стійкості за рівняннями першого наближення, є недостатнім для повного дослідження стійкості нелінійних систем. Унаслідок цього для дослідження стійкості “у великому” і “у цілому” використовують спеціальні методи, до яких належать другий (прямий) метод Ляпунова та критерій стійкості Попова.

Другий (прямий) метод Ляпунова. Метод ґрунтується на побудові спеціальних функцій Ляпунова, які дозволяють отримати достатні умови стійкості рівноваги у великому. Дані функції V мають зміст відстані у спеціальному просторі станів між досліджуваним незбуреним і збуреним рухами. Якщо з часом ця функція спадає, тобто 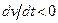, то незбурений рух стійкий, а при - нестійкий.

Дослідження стійкості зводиться до аналізу швидкості зміни функції V. Умови стійкості сформульовані у двох теоремах Ляпунова.

Теорема 1. Якщо існує знаковизначена функція , похідна якої за часом у силу диференціальних рівнянь руху є знакопостійною функцією протилежного з V знаку, або тотожно дорівнює нулю, то незбурений рух стійкий.

Теорема 2. Якщо, крім того, функція знаковизначена, то незбурений рух стійкий асимптотично.

Відзначимо, що знакопостійною називається функція, яка набуває при всіх значеннях своїх аргументів тільки значення одного знаку або нульове значення. Знаковизначеною називається знакопостійна функція, яка набуває нульове значення тільки при нульовому значенні всіх її аргументів (на початку координат).

Складність даного методу полягає у тому, що задача вірного вибору функції Ляпунова пов’язана зі складнощами. Відсутні загальні методи побудови цих функцій. Більше того, зустрічаються випадки, коли система є стійкою, а внаслідок невірно вибраної функції Ляпунова цей факт установити не вдається. У такому випадку для розв’язання технічних задач метод Ляпунова не є досить ефективним.

Дата добавления: 2015-10-29