Зображення процесів на фазовій площині

Якщо рівняння системи представлені у нормальній формі, то вектор стану системи однозначно визначає її стан. Кожному стану системи в просторі станів відповідає точка. Точка, яка відповідає поточному стану системи називається зображуючою точкою. При зміні стану зображуюча точка описує траекторію. Ця траекторія називається фазовою траекторією. Сукупність фазових траекторій, яка відповідає різним можливим початковим умовам, називається фазовим портретом.

Наочно фазову траекторію та фазовий портрет можна представити у випадку двомірного фазового простору. Двомірний фазовий простір називається фазовою площиною.

Фазова площина – це координатна площина, в якій по осях координат відкладаються дві змінні (фазові координати), які однозначно визначають стан системи другого порядку. Метод аналізу та синтезу системи управління, який базується на побудові фазового портрета, називається методом фазової площини.

Через будь-яку точку фазового простору може проходити лише одна траекторія. Однак, на фазовій площині існують особливі точки – точки в яких фазова швидкість рівна нулю, а отже це точки які є положенням рівноваги системи. Через особливі точки може проходити більше одної фазової траекторії.

Часто при зображенні процесів на фазовій площині за фазову координату , яку відкладають по осі ординат, приймають похідну координати 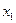, що відкладається по осі абсцис. В цьому випадку диференціальне рівняння фазових траекторій матиме вигляд:

.

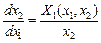Тоді фазові траекторії матимуть наступні властивості. У верхній півплощині зображуюча точка рухається зліва направо, оскільки 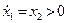та 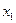зростає. В нижній півплощині, навпаки, зображуюча точка рухається справа наліво так як 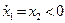та 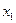спадає. На осі абсцис (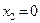) похідна (за винятком точок рівноваги), і тому фазові траекторії перетинають вісь абсцис під прямим кутом.

Фазові портрети нелінійних систем характеризуються більшим різномаїттям, ніж фазові портрети лінійних систем. Однак типи особливих точок лінійних та нелінійних систем співпадають. Тут маються на увазі ті особливі точки, в околі яких рівняння нелінійних систем допускають лінеаризацію.

Дата добавления: 2015-10-29