Двовимірне дискретне пряме й зворотне перетворення Фур'є

Синтаксис:

Y=fft2(X) X=ifft2(Y)

Y=fft2(X,m,n) X=ifft2(Y,m,n)

Опис:

Функція Y=fft2(X) обчислює для масиву даних X двовимірне дискретне перетворення Фур'є. Якщо масив X двовимірний, обчислюється дискретне перетворення для кожного стовпця.

Функція Y=fft(X,n) обчислює n-крапкове дискретне перетворення Фур'є. Якщо length(X) < n, то відсутні рядки масиву X заповнюються нулями; якщо length(X) > n, те зайві рядки віддаляються.

Функція X=ifft(Y) обчислює зворотне перетворення Фур'є для масиву Y.

Функція X=ifft(Y,n)обчислює n-крапкове зворотне перетворення Фур'є для масиву Y.

Приклади:

Розглянемо той же приклад, що й для функції fft, але сформуємо 2 вхідні послідовності (рис. 4):

t=0:0.001:0.6;

x=sin(2*pi*50*t) + sin(2*pi*120*t);

y1=x+2*randn(size(t));

y2=x+2*randn(size(t));

y=[y1;y2];

plot(y(1,1:50)),hold on, plot(y(2,1:50)), grid, hold off

Застосуємо двовимірне перетворення Фур'є для сигналу y на основі 512 крапок і побудуємо графік спектральної щільності (рис. 5). Тепер можна виділити 2 частоти, на яких амплітуда спектра максимальна. Це частоти – 100/2Гц й 240/2Гц.

Y fft2(y, 2, 512);

Pyy=Y.*conj(Y)/512;

f=1000*(0:255)/512;

figure(2), plot(f,Pyy(1:256)), grid

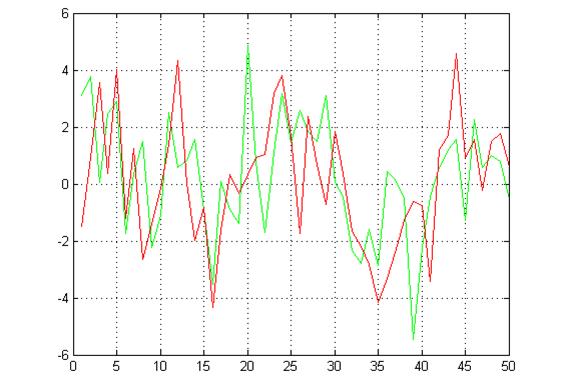
Рис. 4

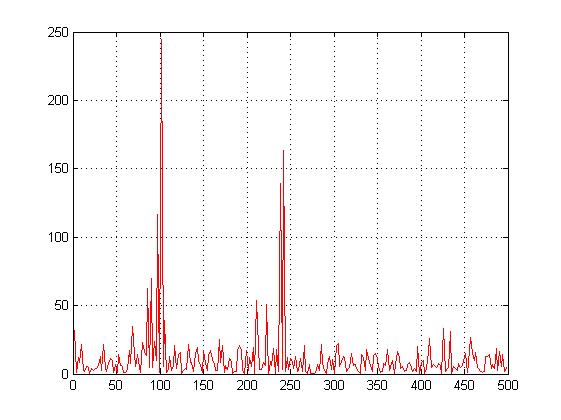
Рис. 5

Алгоритм:

Двовимірне дискретне перетворення пов'язане з одномірним дискретним перетворенням Фур'є в такий спосіб:

fft2(X)=fft(fft(X).’).’

Порядок виконання роботи

1. Ознайомитись з видами перетворень Фур’є та методами реалізації перетворень за допомогою вбудованих функцій математичного пакету Matlab.

2. Згенерувати сигнал передачі даних, що зашумлений перешкодами. Функція, яка описує передаючий сигнал із перешкодами задана у таблиці 1. Сигнал надходять із частотою 1000 Гц, який містить регулярні складові із частотами 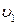, 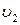і включають випадкову адитивну компоненту з нульовим середнім значенням. Передача проводиться протягом проміжку часу t.

3. За допомогою перетворення Фур’є виділити частоти регулярних складових сигналу, зашумленого перешкодами.

4. Зробити висновки.

Зміст звіту

Звіт повинен містити тему завдання згідно варіанта, відповідні розрахунки та лістинг програмного коду виконання завдання, відповідно до того, як наведено в прикладі. Повині бути описані дії та хід виконання роботи. Після закінчення виконання завдання, по отриманим даним зробити висновки.

Таблиця 1

Дані для формування сигналу

№ п/п	Вид сигналу (функція)	Частоти регулярних складових сигналу, Гц	Час передачі, сек.
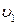
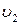
		t
1.		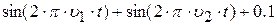		0.8
2.		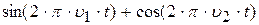		0.6
3.		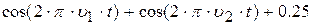		0.8
4.		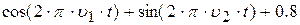		0.6
5.		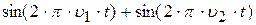		0.8
6.		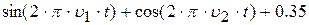		0.6
7.		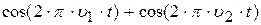		0.8
8.		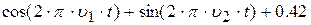		0.6
9.		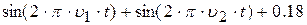		0.4
10.		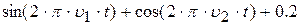		0.8

Продовження таблиці 1

№ п/п	Вид сигналу (функція)	Частоти регулярних складових сигналу, Гц	Час передачі, сек.
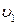
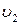
		t
11.		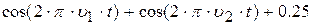		0.6
12.		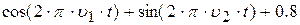		0.6
13.		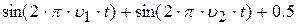		0.8
14.		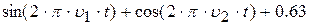		0.6
15.		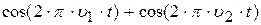		0.8
16.		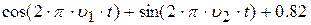		0.6
17.		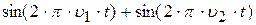		0.8
18.		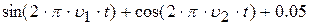		0.6
19.		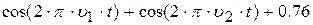		0.6
20.				0.8
21.		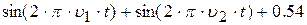		0.6
22.		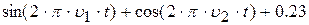		0.8
23.		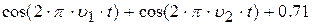		0.6
24.		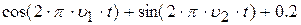		0.8
25.				0.8
26.		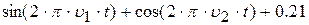		0.6
27.		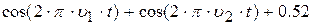		0.8
28.		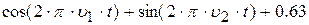		0.6
29.		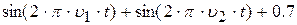		0.8
30.		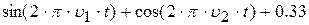		0.6

Контрольні запитання

1. Поясніть відмінності між видами перетворень Фур'є.

2. Дайте характеристику швидкого перетворення Фур'є.

3. Охарактеризуйте дискретне перетворення Фур'є?

4. Поясніть зворотне перетворення Фур'є.

5. Поясніть одновимірне та двовимірне перетворення Фур'є.

Дата добавления: 2015-10-24