Теоретична частина. Цифрова обробка сигналів (ЦОС, DSP – англ

Цифрова обробка сигналів (ЦОС, DSP – англ. Digital signal processing), – перетворення сигналів, представлених у цифровій формі.

Будь-який безперервний (аналоговий) сигнал S (t) може бути підданий дискретизації за часом і квантуванню за рівнем (оцифровка), тобто представлений у цифровій формі. Якщо частота дискретизації сигналу F _d не менше, ніж подвоєна найвища частота в спектрі сигналу F _max (тобто ), то отриманий дискретний сигнал S (k) еквівалентний сигналу S (t) (див. теорему Котельникова). За допомогою математичних алгоритмів S (k) перетворюється в деякий інший сигнал S 1(k) має відповідні властивості. Процес перетворення сигналів називається фільтрацією, а пристрій, що виконує фільтрацію називається фільтр. Оскільки відліки сигналів надходять з постійною швидкістю F _d, фільтр повинен встигати обробляти поточний відлік до надходження наступного (частіше – до надходження наступних n відліків, де n – затримка фільтру), тобто обробляти сигнал в реальному часі. Для обробки сигналів (фільтрації) в реальному часі застосовують спеціальні обчислювальні пристрої – цифрові сигнальні процесори.

Все це повністю стосується не тільки безперервних сигналів а й переривчастих, а також сигналів, записаних на запам'ятовуючі пристрої. В останньому випадку швидкість обробки непринципова, тому що при повільній обробці дані не будуть втрачені.

Розрізняють методи обробки сигналів у часовій (англ. time domain) і в частотній (англ. frequency domain) області. Еквівалентність частотно-часових перетворень однозначно визначається через перетворення Фур'є.

Обробка сигналів у часовій області широко використовується в сучасній електронних осцилографах і в цифрових осцилографах. А для подання сигналів в частотній області використовуються цифрові аналізатори спектру. Для вивчення математичних аспектів обробки сигналів використовуються пакети розширення (найчастіше під ім'ям Signal Processing) систем комп'ютерної математики Matlab, MathCAD, Mathematica, Maple та ін.

В останні роки при обробці сигналів і зображень широко використовується новий математичний базис подання сигналів за допомогою "коротких хвиль" - вейвлетів. З його допомогою можуть оброблятися нестаціонарні сигнали, сигнали з розривами та іншими особливостями і сигнали у вигляді пачок.

Отже, в ЦОС вивчаються два типи сигналів:

– дискретнийсигнал – дискретний за часом та неперервний за станом (рис. 1а);

– цифровийсигнал – дискретний за часом і квантований за стоном (рис. 1б).

Також, в теорії ОС виділяють поняття квантового сигналу – коли відбувається розбиття діапазону значень безперервної або дискретної величини за часом на кінцеве число інтервалів (рис. 1в).

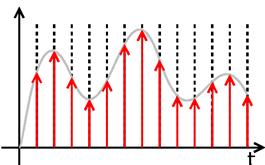
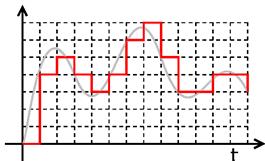
а) б)

в)

Рис. 1

В теорії ЦОС прийнято образно розділяти операції дискретизації та квантування за рівнем. Рахуючи операцію квантування відсутньою, вивчаються дискретні сигнали та лінійні дискретні системи (ЛДС), а потім, окремо, ­– ефекти нелінійної операції квантування.

Таким чином, під дискретним сигналом розуміється послідовність чисел нескінченної розрядності – послідовність x (nT) = x (n), де nT – дискретний час, Т – період дискретизації, а n = nT / T – дискретний нормований час.

Аналогічно, під цифровим сигналом розуміється послідовність чисел скінченної розрядності – квантована послідовність або .

Терміни «дискретний сигнал» та «послідовність» використовують в тотожному смислі.

Випадкові (стохастичні) дискретні сигнали ототожнюються з послідовностями випадкових чисел ­– випадковими (або стохастичними) послідовностями.

Оцифровка (англ. digitization) – представлення об'єкта, зображення або сигналу (звичайно – аналогового) в дискретний, за допомогою набору цифрових вимірів.

Для оцифровки об'єкт піддається модуляції (в одному або декількох вимірах, наприклад, в одному вимірі для звуку, і в двох для растрового зображення) і аналогово-цифрового перетворення кінцевих рівнів.

Отриманий в результаті оцифровки масив даних («цифрове подання» оригінальному об'єкта) може використовуватися комп'ютером для подальшої обробки, передачі по цифрових каналах, збереження на цифровий носій. Перед передачею або збереженням, цифрове подання, як правило, піддається фільтрації та кодуванню для зменшення обсягу.

Дискретизація – це процес переведення безперервного аналогового сигналу в дискретний або дискретно-безперервний сигнал. Зворотний процес називається відновленням. При дискретизації тільки за часом, безперервний аналоговий сигнал замінюється послідовністю відліків, величина яких може бути рівною значенню сигналу в даний момент часу. Можливість точного відтворення такого подання залежить від інтервалу часу між відліками Δ t. Відповідно до теореми Котельникова:

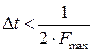
де F _max – найбільша частота спектру сигналу.

Частота дискретизації (модуляції, або семплювання) – частота взяття відліків безперервного в часі сигналу при його дискретизації (зокрема, аналого-цифровим перетворювачем). Вимірюється в Герцах.

Термін застосовується і при зворотному, цифро-аналоговому перетворенні, особливо якщо частота дискретизації прямого та зворотного перетворення обрана різною (Даний прийом, називається також «масштабуванням часу», зустрічається, наприклад, при аналізі наднизькочастотних звуків, що видаються морськими тваринами).

Чим вище частота дискретизації, тим більш широкий спектр сигналу може бути представлений у дискретному сигналі. Як випливає з теореми Котельникова, для того щоб однозначно відновити початковий сигнал, частота дискретизації повинна більш ніж у два рази перевищувати найбільшу частоту в спектрі сигналу.

Квантування (англ. quantization) – в обчислювальній техніці, це розбиття діапазону значень безперервної або дискретної величини на кінцеве число інтервалів. Існує також векторне квантування – розбиття простору можливих значень векторної величини на кінцеве число областей. Квантування часто використовується при обробці сигналів, у тому числі при стисненні звуку та зображення. Найпростішим видом квантування є розподіл цілочисельного значення на натуральне число, що називається коефіцієнтом квантування.

Однорідне (лінійне) квантування - розбиття діапазону значень на відрізки рівної довжини. Його можна представляти як поділ вихідного значення на постійну величину (крок квантування) і взяття цілої частини від часткового:

.

Не слід плутати квантування з дискретизацією (і, відповідно, крок квантування з частотою дискретизації). При дискретизації що змінюється в часі величина (сигнал) вимірюється із заданою частотою (частотою дискретизації), таким чином, дискретизація розбиває сигнал з тимчасової складової (на графіку – по горизонталі). Квантування ж призводить сигнал до заданих значень, тобто, розбиває за рівнем сигналу (на графіку – по вертикалі). Сигнал, до якого застосовані дискретизація і квантування, називається цифровим.

При оцифруванні сигналу рівень квантування називають також глибиною дискретизації або бітністю. Глибина дискретизації вимірюється в бітах і позначає кількість біт, що виражають амплітуду сигналу. Чим більше глибина дискретизації, тим точніше цифровий сигнал відповідає аналоговому. У випадку однорідного квантування глибину дискретизації називають також динамічним діапазоном і вимірюють в децибелах (1 біт ≈ 6 дБ).

Розрізнюють квантування неперервного сигналу за часом і за рівнем. Перше реалізується за допомогою ім­пульсного модулятора, якщо миттєві дискретні значення неперервного сигналу V* (t) утворюються через сталий період Т_о його квантування.

При квантуванні за рівнем виділяються миттєві зна­чення неперервного сигналу v* (t) на фіксованих дискрет­них рівнях у довільні моменти часу (рис. 2). Ці фіксовані рівні сигналу звичайно стоять один від одного на ста­лому інтервалі, які називаються – кроком квантування.

Рис. 2

Квантування за рівнем – представлення величини відліків цифровими сигналами. Для квантування в двійковому коді діапазон напруги сигналу від U _min до U _max ділиться на 2 ⁿ інтервалів. Величина отриманого інтервалу (кроку квантування): .

Кожному інтервалу присвоюється n -розрядний двійковий код – номер інтервалу, записаний двійковим числом. Кожному відліку сигналу присвоюється код того інтервалу, в який потрапляє значення напруги цього відліку. Таким чином, аналоговий сигнал представляється послідовністю двійкових чисел, які відповідають величині сигналу в певні моменти часу, тобто цифровим сигналом. При цьому кожне двійкове число представляється послідовністю імпульсів високого (1) і низького (0) рівня.

У цифрових системах керування здійснюється кванту­вання неперервних сигналів за часом і рівнем, коли вони замінюються дискретними за рівнем значеннями, най­ближчими до значень неперервних сигналів у певні дис­кретні моменти часу, розділені періодом квантування Т_о. При цьому інтервал квантування сигналів за рівнем s ви­значається значущістю молодшого розряду двійкового цифрового коду мікро ЕОМ. Кількість розрядів у коді чисел різних мікро ЕОМ дорівнює 8-16. Тому з достат­ньою для практичних цілей точністю похибками кванту­вання неперервних сигналів за рівнем сучасних мікро ЕОМ можна знехтувати, через що далі розглядатимемо тільки сигнали, квантовані за часом.

При квантуванні неперервного сигналу v(t) за часом із сталим періодом квантування Т_о дістаємо модульовану за амплітудою дискретну функцію v*(t), яку можна запи­сати у вигляді:

(1)

де n = 0, 1, 2, ….

Решітчасті функції. Теоретично вихідна координата v*(f) найпростішого імпульсного модулятора може бути подана у вигляді послідовності дельта-функцій, площа яких становить:

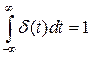(2)

Послідовність імпульсів v*(t) на виході імпульсного модулятора, що мають площу v(t) t_i можна наближено замінити ідеальними імпульсами δ(t) такої самої площі. Введення ідеального імпульсного модулятора, який формує дельта-імпульси, дає змогу значно спростити математичний опис процесу квантування неперервного сигналу, ко­ли припустити, що площі реальних і відповідних ідеаль­них імпульсів однакові. Вважаючи при цьому дійсною не­рівність , послідовність ідеальних імпульсів на виході імпульсного модулятора можна описати виразом:

(3)

де – дельта-функція, зміщена на час пТ₀.

Введемо поняття решітчастої функції v[nT₀], значення якої в дискретні моменти часу t = пТ₀ становлять 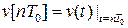. При визначенні цієї функції здійснюється заміна неперервного за часом сигналу по­слідовністю чисел, які є його значеннями в певні моменти часу.

Зворотна задача формування неперервної функції v(t) з решітчастої v [ пТ₀ ]не може бути розв'язана однозначно, тому що одній решітчастій функції може відповідати без­ліч обвідних неперервних функцій, збіжних з дискретни­ми значеннями решітчастої функції.

Втрати інформації при квантуванні. У проміжках між імпульсами характер зміни неперервного сигналу v(t) залишається невідомим. Тому при проходженні останнього через імпуль­сний модулятор втрачає­ться частина інформації, що міститься в цьому сигналі. Щоб при його квантуванні цього не було, необхідно зменшити період квантування Т_о в разі зростання швидкості зміни функції v(t).

Розглянемо фундаментальну теорему Котельникова про вибір періоду квантування неперервного сигналу залежно від його спектра.

Теорема Котельникова. Функція часу v(t), яка не містить гармо­нічних складових з частотами, вищими від частоти 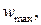повністю визначається своїми значеннями в моменти часу nТ_о, що стоять один від одного на періоди:

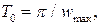(4)

тобто частота квантування має бути вибрана відповідно до умови . У цьому випадку дискретна решітчаста функція точно відобразить неперервну функцію:

(5)

і втрати інформації при її квантуванні не буде.

На підставі теореми Котельникова можна зробити вис­новок, що коли неперервний сигнал v(t) не містить гармо­нічних складових з частотою, вищою від 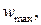то при його квантуванні з періодом дискретна решітчаста функція точно відобразить неперервну функцію, зав­дяки чому втрати інформації при її квантуванні не буде.

Екстраполятор нульового порядку. При реалізації імпульсних систем керування на основі мікро ЕОМ після імпульсного модулятора встановлюють де­модулятор або формуючий елемент, який фік­сує вихідний сигнал імпульсного модулятора на весь пе­ріод квантування Т_о неперервного сигналу. Такі формуючі елементи називаються екстраполяторами або фіксаторами нульового порядку.

При подаванні на вхід екстраполятора нульового по­рядку одиничного імпульсу його вагова функція опису­ється рівнянням: , застосував­ши до якого перетворення Лапласа, дістанемо передаточну функцію екстраполятора:

(6)

Різницеві рівняння. Для математичного опису динамі­ки дискретних систем автоматичного керування викорис­товують різницеві рівняння, які є аналогами диференці­альних рівнянь. Такі рівняння визначають співвідношен­ня між дискретною решітчастою функцією у [ пТ₀ ]та її різницями різних порядків. Перехід від диференціальних рівнянь до різницевих ґрунтується на заміні похідних різницями відповідних порядків. У таблиці 1 наведено співвідношення для заміни похідних різницями. При цьо­му решітчасті функції записуються в більш компактному вигляді, а саме: тощо.

З використанням зазначених співвідношень різницеве рівняння, що відповідає диференціальному рівнянню k -го порядку, можна записати у вигляді:

де y_n – шукана решітчаста функція, яка є розв’язком різ­ницевого рівняння; и_п – відома решітчаста функція.

Диференціальне рівняння можна розглядати як гра­ничний вираз різницевого рівняння, коли період кван­тування Т_о неперервного сигналу прямує до нуля.

Дискретне перетворення Лапласа. Розглянемо пере­творення Лапласа для одиничної решітчастої функції 1[ пТ₀ ], яку можна подати у вигляді такої суми:

де — імпульси одиничної амплітуди нескінченно малої тривалості.

Застосувавши до правої частини цього рівняння зви­чайне перетворення Лапласа, дістанемо зображення оди­ничної решітчастої функції:

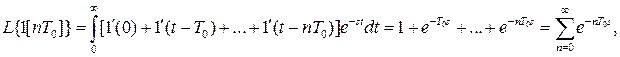
яке відповідає інтегралу.

Якщо замість одиничної 1[ пТ₀ ]використати довільну решітчасту функцію х [ пТ₀ ], то дискретне перетворення Лапласа матиме вигляд:

(7)

яке є перетворенням Лапласа решітчастої функції. При цьому 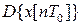– функція оператора , де – комплексна змінна.

Таблиця 1

Дата добавления: 2015-10-24