Співвідношення для заміни похідних різницями

№ пор.	Неперервна функція	Дискретна функція
k	Перша похідна     Друга похідна     …   Похідна k -го порядку	Різниця першого порядку       Різниця другого порядку         …   Різниця k -го порядку

Дискретне перетворення Фур'є (ДПФ) (англ.. DFT, Discrete Fourier Transform) – це пара взаємно однозначних перетворень – дискретних рядів Фур'є, являється одним з перетворень, яке широко застосовуваних у алгоритмах цифрової обробки сигналів (його модифікації застосовуються в стисненні звуку в MP3, стиснення зображень в jpg, тощо), а також в інших областях, пов'язаних з аналізом частот в дискретному (наприклад, оцифрованому аналоговому) сигналі.

Дискретне перетворення Фур'є вимагає для входу дискретну функцію. Такі функції часто створюються шляхом дискретизації (вибірки значень з безперервних функцій). Дискретні перетворення Фур'є допомагають вирішувати приватні диференціальні рівняння і виконувати такі операції, як згортки. Дискретні перетворення Фур'є також активно використовуються в статистиці, при аналізі часових рядів. Перетворення бувають одномірні, двовимірні і навіть тривимірні.

Формули перетворень:

Пряме перетворення:

де k – дискретна нормована частота , D w – період дискретизації за частотою, N – точкова послідовність – періодична послідовність з періодом N в області дискретного нормованого часу;

Зворотне перетворення:

де n – дискретний нормований час , N – періодична послідовність з періодом N в області дискретного нормованого часу.

Позначення:

N – кількість значень сигналу, виміряних за період, а також кількість компонентів розкладу;

– Виміряні значення сигналу (в дискретних тимчасових точках з номерами , які є вхідними даними для прямого перетворення і вихідними для зворотного;

– N комплексних амплітуд синусоїдальних сигналів, що складають вихідний сигнал; є вихідними даними для прямого перетворення і вхідними для зворотного; оскільки амплітуди комплексні, то вони позначають одночасно і амплітуду та фазу;

– звичайна (речова) амплітуда k -го синусоїдальної сигналу;

arg (X_k) – фаза k -го синусоїдальної сигналу (аргумент комплексного числа);

k – частота k -го сигналу, рівна , Де T – період часу, протягом якого бралися вхідні дані.

З останнього видно, що перетворення розкладає сигнал на синусоїдальні складові (які називаються гармоніками) з частотами від N коливань за період до одного коливання за період. Оскільки частота дискретизації сама по собі дорівнює N відліків за період, то високочастотні складові не можуть бути коректно відображені - виникає муаром ефект. Це призводить до того, що перша половина з N комплексних амплітуд, фактично, є дзеркальним відображенням друга і не несе значного сенсу.

Зміст роботи

Для виконання даної лабораторної роботи на ПК, повинен бути встановлений математичний пакет – Matlab 6 або пізнішої версії та додаток до математичного пакету для обробки сигналів – Signal Processing Toolbox. А також володіти поняттями дискретизації та квантування сигналів, знати поняття дискретного прямого та зворотнього перетворення Фур’є та вміти їх застосувати.

Оскільки послідовність чисел нескінченної розрядності представити в Matlab неможливо, тому під дискретним сигналом умовно приймають послідовність чисел максимальної розрядності типу double, з якими Matlab по замовчуванню виконуються внутрішні операції.

В Matlab послідовності можуть представлятись наступним чином:

Одним вектором, елементи якого відповідають відлікам послідовності, а їх індекси ­– значенням дискретного нормованого часу, наприклад (рис. 3а):

x=[1 3 -7 0 2 -1 8 0 0 -2 -1 4 8];

subplot(2,2,1),stem(x,'fill','MarkerSize',3),grid

Двома векторами, елементи одного з яких відповідають значенням дискретного нормованого часу, а другого ­– відлікам послідовності, наприклад (рис. 3б):

n=0:12; x=n.^2;

subplot(2,2,2),stem(n,x,'fill','MarkerSize',3),grid

Рис. 3

Матрицею, k-й стовпець, який відповідає k -й послідовності, а індекси елементів стовпця – значенням дискретного нормованого часу, наприклад (рис. 3в):

x=[0 -1;-4 7;3 2;9 1;-2 3;2 -5;3 -1];

subplot(2,2,3),stem(x,'fill','MarkerSize',3),grid;

subplot(2,2,3), hold on, plot(x(:,1));

subplot(2,2,3), hold on, plot(x(:,2),':');

Вектором та матрицею, де елементи вектора відповідають значенням дискретного нормованого часу, однакового для всіх послідовностей, а k -й стовпець – k -й послідовності, наприклад (рис. 3г):

n=0:6;

x=[0 -1;-4 7;3 2;9 1;-2 3;2 -5;3 1];

subplot(2,2,4),stem(n,x,'fill','MarkerSize',3),grid;

subplot(2,2,4), hold on, plot(n,x(:,1));

subplot(2,2,4), hold on, plot(n,x(:,2),':');

де елементи вектора n відповідають значенням дискретного нормованого часу.

Представлення послідовностей у вигляді матриць є зручним при одночасній та однотипній обробці декількох дискретних сигналів, заданих на однаковому інтервалі дискретного часу.

В ЦОС виділяють декілька типових послідовностей:

Цифровий одиничний імпульс:

записується як матриця рядок з нулів.

Цифровий одиничний стрибок:

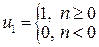
записується як матриця рядок з одиниць.

Дискретна експонента:

представляється вектором x заданої довжини.

Дискретний комплексний гармонічний сигнал:

Отже, згенеруємо аналоговий та дискретний гармонічний сигнал sin(wt)+cos(wt), де w = 1.5 – частота синусоїди, а t = 32 – вектор аналогового моменту часу (кількість відрахунків). За допомогою дискретного перетворення Фур'є (ДПФ) виділимо піки частот, які являються частотами регулярних складових сигналу, тобто ту частину спектру сигналу, що має відповідну повторюваність, за допомогою яких можна спростити та пришвидшити передачу інформації.

td=(0:31)';

t=(0:0.1:32)';

w=1.5

as=sin(w*t)+cos(w*t);

ds=sin(w*td)+cos(w*td);

subplot(2,1,1), plot(t,as,'-');

hold on;

stem(td,ds,'filled','MarkerSize',5);

hold off;

xlim([t(1) t(end)]);

subplot(2,1,2);

stem(td, abs(fft(ds)),'filled','MarkerSize',5)

xlim([t(1) t(end)]);

subplot(2,1,2);

stem(td, abs(fft(sd)),'filled','MarkerSize',5)

xlim([t(1) t(end)]);

На приведених графіку згенерованого сигналу (рис. 4а) та графіку дискретного перетворення Фур'є (рис. 4б). На графіку, де зображене ДПФ, ми можемо спостерігати два піки частот, які являються частотами регулярних складових сигналу sin(wt)+cos(wt). Дані піки частот показують частину сигналу, що має повторюваність протягом всього проміжку трансляції сигналу.

При передачі певної інформації, дана властивість перетворення дозволяє виконувати стиснення (компресію) інформації яка передається, що значно пришвидшує передачу даних, та зменшує об’єм інформації, що передається.

Проаналізуємо графік (рис. 4б) дискретного перетворення Фур'є далі. Тут ми можемо спостерігати розтікання спектру, яке проявляється в тому, що при обчисленні ДПФ синусоїди з частотою, яка не співпадає з жодною з частот аналізу, замість чіткого піку ми отримуємо складний спектр, в якому в загальному випадку можуть міститись всі можливі частоти. Причина розтікання спектра полягає в тому, що ДПФ неявно розуміється періодичне продовження аналізованого фрагмента сигналу. Якщо на розглянутому проміжку укладається ціле число періодів синусоїди (це еквівалентно умові збігу її частоти з однієї із частот аналізу), періодично продовжений сигнал також буде безперервною синусоїдою, у спектрі якої втримується єдина частота. Якщо ж число періодів на інтервалі аналізу не є цілим, при періодичному продовженні сигналу безперервність синусоїди виявиться порушеною й спектр «розтечеться».

Рис. 4

Для боротьби з розтіканням спектру використаються вагові, або віконні, функції (window). При цьому сигнал перед обчисленням ДПФ множиться на деяку функцію, що спадає від середини до країв. Це дозволяє послабити вплив розривів, що виникають на стиках фрагментів сигналу при його періодичному продовженні.

Синтаксис:

w = hann(n)

w = hann(n,'sflag')

Опис:

Повертає n -крапкове симетричне вікно Ханна у вигляді вектора-стовпця w. Вхідний параметр n повинен бути цілим позитивним числом. Коефіцієнти вікна Ханна розраховуються таким чином:

w = hann(n,'sflag') Повертає n -крапкове вікно Ханна, дискретні крапки розрахунку якого визначаються строковим вхідним параметром 'sflag', що має два можливих значення: 'periodic' й 'symmetric' (останній варіант прийнятий по замовчуванню). Якщо обрано варіант 'periodic', функція hann розраховує симетричне вікно довжини n +1 і повертає його перші n крапок.

sw = as.*hann(length(as));

sdw = ds.*hann(length(ds),'periodic');

subplot(2,1,1), plot(t,sw,'-');

hold on;

stem(td,sdw,'filled','MarkerSize',5);

hold off;

xlim([t(1) t(end)]);

subplot(2,1,2);

stem(td, abs(fft(sdw)),'filled','MarkerSize',5);

xlim([t(1) t(end)]);

На рис. 5 показаний сигнал (рис. 5а) і модуль його ДПФ (рис. 5б) при використанні вікна Ханна (функція hann). Видно, що використання вагової функції дозволило істотно послабити побічні спектральні складові – правда, за рахунок розширення спектральних піків. Останнє, на жаль, неминуче.

Рис. 5

Дата добавления: 2015-10-24