Оцінка точності за різницями подвійних нерівноточних| вимірів

Розглянемо|розглядуватимемо| n пар подвійних нерівноточних| вимірів|вимірів| об'єктів однакового роду. Формально запишемо

де знак «» позначає приналежність ваги , до кожного вимірювання|виміру| виділених пар. При цьому в кожній парі вимірювання|виміру| рівноточні|.

Така ситуація має місце при порівнянні результатів лінійних вимірів|вимірів| полігонометричних| (теодолітних|) ходів, де лінії мають різну довжину, або при порівнянні результатів подвійного нівелювання у ходах різної довжини.

Складемо для кожної пари (7.13) різниці

які є|з'являються| істинними похибками.

Для ваги різниці запишемо вираз|вираження| із урахуванням|з врахуванням| основної теореми теорії похибок і формули (6.6)

Здійснюючи нескладні перетворення отриманої|одержувати| формули, знайдемо вагу різниці кожного вимірювання

Визначимо середню квадратичну| похибку одиниці ваги, скориставшись при цьому виразом|вираженням| (6.41) і підставивши в нього вираз|вираження| (7.15), отримаємо|одержуватимемо| формулу

або спрощуючи її, маємо

Відповідно середня квадратична похибка результату одного вимірювання з вагою p_i визначається на підставі (6.8) шляхом заміни в цій формулі стандарту одиниці ваги на середню квадратичну похибку одиниці ваги µ. Тоді отримаємо

Середня квадратична похибка арифметичної середини по кожній парі (7.14) обчислюється за формулою

Надійність оцінок µ і m_i:

Формули (7.16 – 7.21) справедливі, якщо різниці d_i не містять істотних систематичних похибок. За наявності систематичних похибок визначають коефіцієнт систематичного впливу, який обчислюється за формулою

де l – довжини вимірюваних ліній для лінійних вимірів|вимірів| і

де L – довжина ходу подвійного нівелювання.

Знайдемо співвідношення, за допомогою яких можна було б обчислити поправки з урахуванням коефіцієнтів систематичного впливу λ_l і λ_L, ∂_i =d_i – λ_l·lдля лінійних вимірів і ∂_i =d_i – λ_L·L для подвійного нівелювання.

З урахуванням поправок обчислимо середню квадратичну| похибку одиниці ваги за формулою

Для оцінювання надійності середньої квадратичної| похибки скористаємося формулою (6.40), підставляючи в неї формулу (7.24).

Середня квадратична похибка виміряної|виміряти| довжини лінії або нівелірного|нівелір| ходу з урахуванням|з врахуванням| формули (7.24) розраховується за формулою

а середнє перевищення по ходу розраховується відповідно до виразу

Надійність оцінок точності вимірів|вимірів| (7.25) і (7.26) визначимо за формулами (7.20) та (7.21). Приведемо приклад|зразок| оцінювання точності подвійних вимірів|вимірів|.

Приклад 7.3. Необхідно оцінити точність результатів подвійного нівелювання 10 ходів, які представлені в табл. 7.3.

Підсумуємо значення другого і третього стовпців табл.7.3, отримаємо [d]=163,0 і [L]=55,0. За формулою (7.23) обчислимо коефіцієнт систематичного впливу на вимірювання:

Для обчислення різниць необхідно обчислити добутки λ_LL і їх значення, з урахуванням знаку, занести до 4-го стовпця табл. 7.3. Сума цих добутків дорівнює [– λL]=163,1.

Таблиця 7.3 – Результати подвійної нівелювання

№ ходів	Різниця d, мм	Довжина ходу L, км.	- λL, мм	∂, мм	∂^2	p∂^2	mi, мм	Мi, мм
	54.2	2.6	-7.7	46.5	2162.2	831.6	20.5	14.5
	54.3	8.2	-24.3	30.0	900.0	109.8	36.4	25.7
	44.0	7.7	-22.8	21.2	449.4	58.4	35.2	24.9
	-13.4	8.7	-25.8	-39.2	1536.6	176.6	37.5	26.5
	-2.9	6.2	-18.4	-21.3	453.7	73.2	31.6	22.3
	54.3	3.5	-10.4	43.9	1927.2	550.6	23.8	16.8
	32.3	2.3	-6.8	25.5	650.2	282.7	19.3	13.6
	-5.5	6.7	-19.9	-25.4	645.2	96.3	32.9	23.3
	-24.8	3.1	-9.2	-34.0		372.9	22.4	15.8
	-29.5	6.0	-17.8	47.3	2237.3	372.8	31.1	22.0
	[ d ]=163,0	[ L ]=55,0

Відомі значення підставимо до формули ∂_i =d_i – λ_L·L_i, що враховує поправку, яка компенсує систематичні похобки кожного ходу подвійного нівелювання. Результати обчислення величин ∂_i умістимо до 5-ого стовпця табл.7.3.

Розрахуємо поправку ∂^*, яка враховує як коефіцієнти систематичного впливу для окремо узятого вимірювання, так і довжини ходу для подвійного нівелювання. Цю поправку обчислимо спочатку перетворивши формулу (7.23) до вигляду [d]= λ_L[L], а потім підставляючи відоме значення [– λL] і обчислене значення λ_L[L]=163,2 до формули ∂^* = λ_L[L]– [λL], отримаємо ∂^* =0,1.

Зважаючи на формулу (6.14) для обчислення ваги перевищення нівелірного ходу розрахуємо 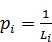для нашого випадку і отримані ваги помножимо на квадрати різниць ∂². Результати занесемо до 7-го стовпця табл.7.3. Підсумуємо отримані результати відповідно до формули [∂²]=2924,9.

Показники оцінки точності результатів вимірів|вимірів|

Обчислимо середню квадратичну|обчислятимемо|| похибку одиниці ваги, яку вважають показником оцінки точності результатів вимірів|вимірів|. Для цього у формулу (7.24) підставимо відомі чисельні значення, отримаємо

|одержуватимемо|Обчислимо середню квадратичну|обчислятимемо|| похибку виміряних|виміряти| довжин ліній або нівелірного|нівелір| ходу для кожного з ходів за формулою (7.27), а результати занесемо до 8-го стовпця табл.7.3

Обчислимо|обчислятимемо| середнє перевищення по ходу враховуючи формулу (7.26) та (6.15) і приводячи|призводити| їх до вигляду|виду|

Показники оцінювання надійності результатів вимірів|вимірів|

Надійність значення показника μ оцінимо з використанням формули (7.19)

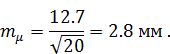
Надійність значень показника m_i оцінимо з використанням формули (7.20) підставляючи до неї результати обчислень (див. 8-й стовпець табл.7.3), отримаємо

Надійність значень показника M_i оцінимо з використанням формули (7.21), підставивши до неї результати обчислень (див. 9-й стовпець табл.7.3), отримаємо

Узагальнимо отримані в процесі математичної обробки результати. З урахуванням виключення систематичної похибки середня квадратична похибка одиниці ваги подвійних вимірів склала 12,7 мм/км., що при сумарному значенні довжин ходів [L]=55,0 км. складає незначну величину. У цьому випадку можна стверджувати, що подвійні вимірювання проведені з достатньою точністю.

Решта показників m_i і M_i характеризують точність подвійних вимірів кожного ходу. Аналіз 8-го і 9-го стовпців табл. 7.3 показують, що найбільш грубий результат отриманий при вимірюванні 4 ходу. Порівнюючи показники точності оцінок і їх надійності, можна стверджувати про достатньо високу точність вимірів і їх надійність.

Таким чином, розглянуті|розглядувати| загальні|спільні| положення|становища| і особливості подвійних вимірів|вимірів|. На цій основі розглянуті|розглядувати| процедури і показники оцінювання точності за різницями подвійних рівноточних| і нерівноточних| вимірів|вимірів|. Показано, що оцінка надійності є|з'являється| складовою частиною оцінювання точності результатів вимірювання|виміру|. Приклади|зразки|, розглянуті|розглядувати| у цьому розділі сприяють кращому засвоєнню логіки математичних перетворень.

Дата добавления: 2015-10-29