Геодезичних вимірів

Завершальною процедурою зрівнювання геодезичних вимірів параметричним способом, як це відомо|показний| із попереднього підрозділу, є оцінка точності зрівняних|урівнювати| значень невідомих. Розглянемо|розглядуватимемо| цю процедуру детально. Як і в математичній обробці однієї величини оцінюватимемо точність декількох невідомих, тобто визначимо їх середні квадратичні похибки| . Розв’язання даної задачі має деякі особливості, що полягають в тому, що поправки , , , …, , 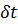– величини залежні. Причому математичному аналізу піддається не одна функція, а декілька.

Оскільки величини , ,…, (див. п.п. 10.1) виміряні|виміряти| незалежно і рівноточно|, їх середні квадратичні похибки| дорівнюють

.

Відповідно будуть рівні і їх ваги , а також середні квадратичні похибки вимірів m і середні квадратичні похибки одиниць ваги μ, .

Звернемося до рівняння (10.18), де елементи матриць Δ і λ є змінними, а елементами зворотної матриці є безперервні функції (10.10), що диференціюються, і відповідно до основної теореми теорії похибок (див. п.п.4.1) характеризуються стандартами даних функцій. Тоді зворотна матриця може бути представлена функціональним визначником матриці Якобі (Якобіаном), елементи якого, є часткові похідні.

Запишемо:

. (10.19)

Підставимо отриману матрицю (10.19), а також матриці Δ і λ у вираз (10.18) і враховуючи властивості операцій над матрицями отримаємо наступне співвідношення:

.

Спрощуючи отриману|одержувати| формулу матимемо:

.(10.20)

Отримана|одержувати| і записана в матричному вигляді формула для розрахунку середньої квадратичної похибки| сукупності поправок за умови рівноточних| вимірів і незалежності поправок , , , …, .

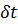Для обчислення точності зрівняних значень невідомих у разі їх залежності виконаємо наступні процедури. Враховуючи, що матриця симетрична, замінимо в ній діагональніелементи на вагові коефіцієнти, величини яких дорівнюють зворотним вагам невідомих

Відмітимо, що діагональні елементи формованої матриці Q завжди позитивні. Недіагональні елементи можуть бути як позитивними, так і негативними. Вони є кореляційними моментами, обумовленими залежністю певних невідомих. Наприклад, елемент і рівний йому елемент слід розглядати як кореляційний момент, обумовлений залежністю величин x і у, тобто .

Позитивне значення свідчить про те, що збільшення або зменшення похибки неминуче приводить до збільшення або зменшення величини 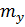. І, навпаки, негативне значення свідчить про те, що збільшення тягне за собою зменшення 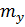, а зменшення – збільшення .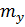

Тоді справедливо записати, що,і .У розгорненому вигляді формула (10.20) набере вигляду

. (10.21)

Звідси витікає, що квадрат середньої квадратичної похибки сукупності невідомих x, у, z,…, t є матрицею, яка отримана множенням квадрата середньої квадратичної похибки m виміряних величин на матрицю Q.

При обчисленні середніх квадратичних похибок невідомих x, у, z,…, t враховуватимемо, що ваги функцій результатів вимірів пов'язані із стандартом і стандартом одиниці ваги співвідношенням (6.8). Тоді справедливо записати наступні співвідношення:

, ,…, . (10.22)

З проведеного аналізу виходить, що хоча величини виміряні рівноточно і незалежно, отримані в результаті зрівнювання значення незалежних величин x, у, z,…, t є нерівноточними і залежними величинами.

Дата добавления: 2015-10-29