Зрівнювання і оцінка точності нерівноточних вимірів

При знаходженні поправок нерівно точних вимірів використовують метод найменших квадратів, тобто враховують умови (9.3),

В цьому випадку функція Лагранжа (див.11.2) приймає вигляд:

Знайдемо часткові похідні від цієї функції за змінними і прирівняємо їх до нуля

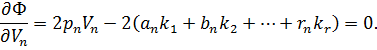
Знайдемо із отриманої системи рівнянь шукані поправки.

Рівняння (11.32) відрізняються від аналогічних їм рівнянь (11.8) для рівноточних вимірів знаменниками, які є вагами в правій частині.

Спростимо рівняння (11.32) і приведемо їх до рівно точного вигляду шляхом нескладних перетворень. Для цього помножимо їх почленно на і введемо наступні позначення

З урахуванням прийнятих позначень системи рівнянь (11.6) і (11.32) можна записати, відповідно, в матричному вигляді:

. (11.34)

Підставимо із (11.34) в формулу (11.33), отримаємо систему нормальних рівнянь корелат

, (11.35)

Яка вирішується добутком отриманого матричного рівняння зліва на обернену матрицю

(11.36)

Підставимо врівняння (11.34) і знайдемо вектор-стовпець поправок .Для отримання вірогідніших поправок необхідно помножити зліва на діагональну матрицю Q, елементи якої дорівнюють і розташовані на головній діагоналі матриці, а всі інші елементи дорівнюють 0.

Емпірична середня квадратична похибка одиниця ваги для нерівно точних вимірів обчислюється за формулою:

Перейдемо до оцінки точності множини функцій, які зрівнюють нерівноточно виміряні величини. Для цього будемо спиратися на доказ основної теореми теорії похибок. Тоді обернена вага сукупності функцій, що має вигляд (11.23) при нерівно точних вимірах буде дорівнювати:

Підставимо в отриманий вираз, аналогічно тому, як це було зроблено в (11.18), значення часткових похідних (11.19) і (11.20), врахуємо прийняті для нерівноточних вимірів позначення ,…, , а також приймемо до уваги вирази (11.33-11.35) і (11.37). Виконаємо відповідні перетворення і операції добутку матриць, як це зроблено в п.11.3. В результаті отримаємо обернені ваги сукупності функцій 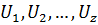нерівноточно виміряних величин

Тоді, враховуючи перетворення, зроблені в п 11.3для отримання формули (11.27), середню квадратичну похибку для сукупності функцій 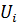, можна записати:

.

Відзначимо, що елементи матриці 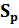мають той же сенс, що і відповідні ним елементи матриці S в формулах (11.27) и (11.28).

Таким чином, розглянута процедура зрівнювання і оцінки точності функцій зрівняних нерівно точних вимірів.

Дата добавления: 2015-10-29