Шикувань|10.1. Постановка задачі. Рівняння поправок

Нехай для визначення значень невідомих x, у, z,…, t виконані рівноточні незалежні виміри . Загальне число невідомих t, загальне число вимірів n. При цьому . Ці умови свідчать про те, що система рівнянь, що відображає процес вимірів є перевизначеною. В даному випадку невідомими можуть бути координати пунктів, висоти реперів та інші фізичні величини, значення яких необхідно визначити, а вимірюваними величинами – горизонтальні напрями, горизонтальні або вертикальні кути, довжини ліній, перевищення тощо. Природно припустити, що між невідомими x, у, z,…, t і вимірюваними величинами існує деяка залежність, яку в загальному вигляді можна представити наступним математичним співвідношенням:

де 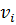- поправки для виміряних значень L_i.

Деталізуємо співвідношення (10.1) і запишемо його у вигляді системи рівнянь поправок:

… (10.2)

Зведемо отриману систему рівнянь (10.2) до вигляду зручного для диференціювання і задоволення умови (9.3), тобто умови мінімізації поправок. Для цього введемо деякі прирости до невідомих і позначимо їх , , ,…, , і так само до поправок, які позначимо , , ,…, 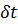. Тоді справедливо записати наступну систему рівнянь:

,

,

, (10.3)

…

.

Підставимо отримані|одержувати| співвідношення (10.3) в систему рівнянь (10.2) і запишемо функцію в загальному виді:

. (10.4)

Для подальшого|дальшого| математичного аналізу отриманого|одержувати| вираження скористаємося процедурами розкладу функції в ряд|лаву| Тейлора. Нагадаємо, що формула Тейлора застосовуються для апроксимації функції многочленами, а лінеаризація рівнянь відбувається|походить| шляхом розкладання в ряд|лаву| Тейлора і відсікання всіх членів вище першого порядку|ладу|. Формула Тейлора і одна з теорем диференціального числення|обчислення| для довідки приведена в додатку|застосуванні| Г.

Припустимо, що функції (10.4) є такими, що їх можна розкласти в ряд Тейлора в границях точок , , ,…, . Оскільки прирости , , ,…, , є малими величинами, то обмежуючись лінійними членами розкладання отримаємо:

де .

Введемо позначення:

Із урахуванням обмежень і введених|запроваджувати| позначень, які обертають статистичні|поважні| члени ряду|лави| |звертають|в малі величини можна записати:

, .

Тоді систему рівнянь (10.2) з урахуванням виконаних|проробити| перетворень можна записати в лінеаризованому виді:

,

,

… (10.7)

.

Таким чином, в отриманих рівняннях невідомими є поправки 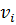для виміряних значень , і прирости поправок , , ,…, для значень параметрів , , ,…, . Тому отримана|одержувати| система параметричних рівнянь (10.7) є недовизначеною, тому що кількість невідомих більша, ніж кількість рівнянь, яка дорівнює n.

Дата добавления: 2015-10-29