Формула розрахунку емпіричної середньої квадратичної| похибки

У п.3 розглянуті|розглядувати| кількісні критерії і чисельні приклади|зразки| апостеріорної оцінки точності ряду|лави| незалежних рівноточних| вимірів|вимірів| однієї величини за дійсними похибками. Цей спосіб є|з'являється|, безумовно, ефективним тільки|лише| тоді, коли у процесі вимірів|вимірів| поруч з|поряд з| результатами вимірів|вимірів| отримують|одержувати| їх дійсні похибки. Проте|однак| у багатьох випадках геодезичної практики дійсні похибки залишаються невідомими. Тому виникає необхідність апостеріорної оцінки точності вимірів|вимірів| за їх результатами.

Наведемо доказ теореми.

Теорема 5.1. Якщо l₁, l₂,…, l_n – результати незалежних рівноточних вимірів, вільних від змінних систематичних похибок, то величина

де v – найймовірніші поправки, є спроможне і незміщене наближення до квадрата стандарту, тобто дисперсії σ² випадкових оцінок вимірюваної величини.

Результати вимірів|вимірів| представимо|уявлятимемо| у вигляді|виді|:

де – постійна систематична похибка; Δ_i – випадкова похибка, Х – дійсне значення вимірюваної величини.

Оскільки|тому що| постійна систематична похибка враховується при обчисленні|підрахунку| арифметичної середини, то справедлива рівність

де Δ _L – дійсна випадкова похибка арифметичної середини.

Віднімемо з отриманого виразу по черзі кожне із системи рівнянь (5.13) і, зважаючи на систему лінійних рівнянь (5.8) 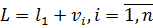отримаємо наступне|одержуватимемо|: . Представимо|уявлятимемо| ці вирази у наступному вигляді|виді|:

Піднесемо, ліві і праві частини|частки| до квадрата, а результати підсумуємо наступним чином:

Підставивши в отриманий вираз формулу (5.7), тобто отримаємо:

Перетворюючи цей вираз отримаємо: 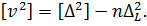У правій частині винесемо за дужку n і поділимо обидві частини рівняння на n-1. У результаті отримаємо

Спочатку доведемо, що права частина отриманого виразу є спроможною оцінкою дисперсії. Для цього перейдемо до межі при n→∞. Скористаємося методами математичного аналізу, зокрема правилом Лопіталя, при розкритті невизначеності яке є складовою правої частини рівняння (5.15), перетворює на одиницю

Друга складова правої частини рівняння (5.15) через першу властивість простої арифметичної середини при n→∞ наближається до нуля

Тоді через властивість розсіювання (2.14) випадкових похибок ліву частину рівняння (5.15) справедливо прирівняти до значення дисперсії σ ²

Таким чином, перша частина|частка| теореми доведена.

Для доказу другої частини|частки| теореми припустимо|передбачатимемо|, що виконано t серій незалежних рівноточних| вимірів

|вимірів|

Для кожної серії вимірів запишемо формулу для розрахунку середньої квадратичної похибки

де Δ – похибка кожного вимірювання в серії, а – похибка i - ї серії вимірів. Підсумуємо отримані вирази і отримаємо формулу

Особливість запису отриманого виразу полягає в тому, що він записаний на змішаній математичній мові, тобто з використанням формального представлення символу суми «[ ]» К.Ф.Гаусса, а також загальноприйнятого в математиці символу суми «∑».

Розділимо почленно все на t і переходячи до межі при t→∞ матимемо

Розглянемо границі у фігурних дужках виразу (5.16). Перша границя згідно з властивості розсіювання дорівнює σ ², оскільки в чисельнику стоїть сума квадратів випадкових похибок, а в знаменнику – їх кількість. Друга границя є границею суми квадратів випадкових похибок арифметичної середини, що ділиться на їх кількість, що згідно властивості розсіювання дорівнює і, зважаючи на другу властивість арифметичної середини (5.3), отримаємо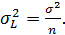

Зробивши відповідні підстановки, знаходимо

|находимо|Отже, оцінка (5.11) є незміщеною. Таким чином, отримано незміщене наближення до стандарту σ, що і потрібно було довести.

Зберігаючи в (5.11) те ж позначення середньої квадратичної похибки m, як і в (3.6), щоб їх якось розрізняти, наближення (5.11) називатимемо емпіричною середньоквадратичною похибкою.

5.3. Послідовність математичної обробки ряду|лави| рівноточних|

Дата добавления: 2015-10-29