Основна теорема теорії похибок

У геодезичній практиці переважно використовуються не окремі безпосередньо зміряні величини, а їх функції, тобто непрямі вимірювання. Так, наприклад, нахил лінії визначають як відношення безпосередньо виміряного перевищення і довжини лінії. Довжина лінії, недоступної для безпосереднього вимірювання, обчислюється із розв’язання трикутника, у якого безпосередньо виміряні базисна сторона і горизонтальні кути. Площу земельної ділянки прямокутної форми обчислюють як добуток безпосередньо виміряної довжини і ширини ділянки. Перелік подібних прикладів можна продовжувати. Звідси виникає завдання оцінювання точності функції виміряних величин за відомими стандартами σ або средньоквадратичними похибками m безпосередньо виміряних аргументів. Для розв’язання цього завдання доведена теорема.

Теорема 4.1. Якщо певна безперервна функція, що диференціюється за всіма аргументами

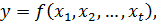(4.1)

аргументи якої x₁, x₂,…, x_t – незалежні результати безпосередніх вимірів певних величин X₁, X₂,…, X_t, виконаних в умовах, що характеризуються стандартами σ₁, σ₂,…, σ_t, то стандарт цієї функції буде дорівнювати

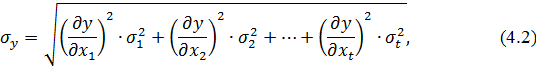
де – частинні похідні функції (4.1) за змінними x₁, x₂,…, x_t,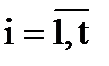

Доказ. З курсу математичного аналізу відомо, що повний диференціал функції (4.1) дорівнює

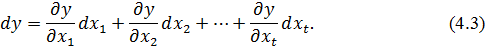
Припустимо, що величини x₁, x₂,…, x_t виміряні n разів. При цьому результати вимірів містять випадкові похибки, які позначимо:

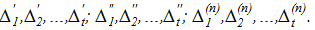
Наочно|наглядний| в графічній формі величини вимірів|вимірів| і їх похибки, ілюструються рис. 4.1.

n-я серія вимірювань

2-я серія вимірювань

1-я серія вимірювань

…

…

…

…

…

…

…

…

Рис. 4.1 – Графічна інтерпретація величин вимірів і їх похибок

Вважаючи, що похибки Δ_і є приростами величин х_і (малими величинами), то на підставі запису повного диференціала (4.3) можна записати систему рівнянь у частинних похідних, де кожне з рівнянь характеризує зміну похибок у серії вимірів величин x₁, x₂,…, x_t

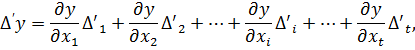
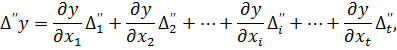
… (4.4)

Відзначимо, що кожен елемент , ,…, , системи рівнянь має константу . Для того, щоб точно оцінити функції виміряних величин y = f (x₁, x₂,…, x_t) з використанням стандарту σ або середньоквадратичної похибки m (див. формулу 2.14 і 3.6) необхідно здійснити наступні перетворення з системою рівнянь (4.4). Звести у квадрат праві та ліві частини кожного з рівнянь. Отримаємо

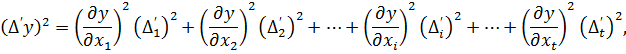
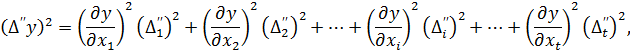
… (4.5)

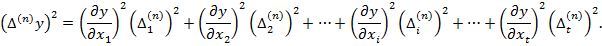
Тепер кожне з рівнянь є сумою квадратів. Для того, щоб привести праві частини рівнянь до вигляду відомих формул скороченого множення многочленів додамо до кожного рівняння суми добутків, що складаються з двох пар у кожному многочлені. Отримаємо

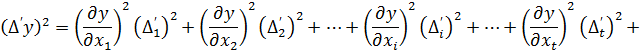
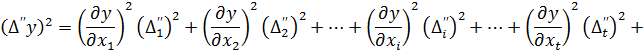
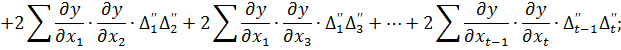
… (4.6)

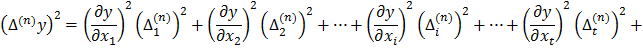
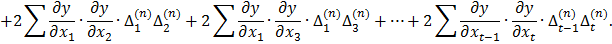
Підсумуємо змінні лівої і правої частини|частки| отриманих|одержувати| многочленів і запишемо їх в символах Гаусса К.Ф.

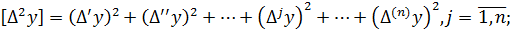
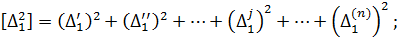
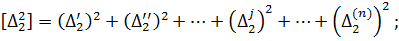
… (4.7)

…

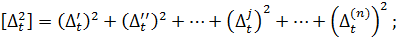
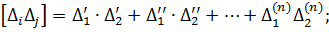
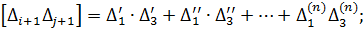
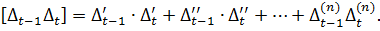
Розділимо отримані суми на n і запишемо остаточний вираз, що враховує всі змінні (похибки Δ_i) системи рівнянь (4.4)

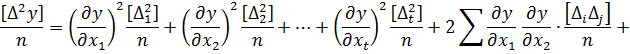
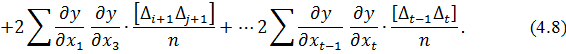
Припускаючи, що n → ∞, знайдемо межі лівої і правої частини отриманого виразу. На основі властивості незалежності (2.13) маємо наступне:

Враховуючи властивість розсіювання (2.14) для правої і лівої частини|частки| рівняння (4.8) справедливо записати

Спростимо вираз (4.8), відкинувши подвійні суми

,

оскільки вираз (4.9) їх перетворює на нуль, і, застосовуючи до його лівої частини граничне значення формули (4.10), а до правої частини – граничні значення формули (4.11) і добувши з них квадратний корінь, отримаємо вираз (4.2), що і потрібно було довести.

Дата добавления: 2015-10-29