Мінімум Нормальні рівняння

На основі отриманої|одержувати| в п.п. 10.1 систем рівнянь (10.7), яка описує лінеаризовану систему поправок покажемо процедуру її нормалізації. Для цього запроваджуватимемо обмеження на число невідомих в системі рівнянь з метою зменшення розмірності вирішуваного|рішати| завдання|задачі|. Вважатимемо|гадатимемо|, що число рівнянь дорівнює n, а число невідомих дорівнює 3. Тоді система рівнянь (10.7) набере вигляду:

,

,

… (10.8)

.

Число надмірних вимірів в даному випадку дорівнює і тому система рівнянь не має єдиного рішення.

Знайдемо для цієї системи мінімум . Для цього виконаємо наступні перетворення. Спочатку зведемо в квадрат праві і ліві частини рівнянь поправок (10.8), а потім результати складемо. Результат запишемо в символах К.Ф. Гаусса

. (10.9)

Для знаходження локального екстремуму отриманої|одержувати| функції, тобто 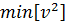візьмемо часткові похідні за невідомими , , і прирівняємо їх до нуля|нуль-індикатора|. Отримаємо|одержуватимемо|:

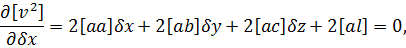
Скоротимо дані вирази на спільний множник 2 і отримаємо|одержуватимемо| систему нормальних рівнянь, в якій число невідомих дорівнює числу рівнянь

(10.10)

Така система рівнянь має єдине рішення і тому її прийнято називати системою нормальних рівнянь.

У отриманій системі рівнянь коефіцієнти при невідомих, які розташовані по головній діагоналі прийнято називати квадратичними. Особливістю отриманої системи рівнянь є те, що коефіцієнти головної діагоналі завжди позитивні, а коефіцієнти при невідомих, розташовані симетрично щодо головної діагоналі, попарно рівні між собою, тобто система рівнянь (10.10) симетрична. Розв’язавши цю систему, знаходимо невідомі , , . Підставивши набутих значень невідомих в систему рівнянь (10.8) можна знайти значення поправок.

Таким чином, описана процедура перетворення системи лінеаризованих рівнянь, яка не має єдиного розв'язання в систему нормальних рівнянь що має єдине розв'язання.

Дата добавления: 2015-10-29