Моделювання роботи ЛДС з використанням різницевого рівняння.

1. На основі власної дати народження записати різницеве рівняння:

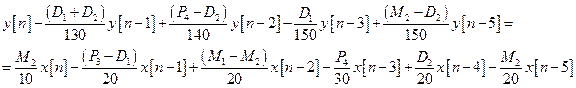
Дата народження: 06.11.1995 В програмі задати вектори a та b коефіцієнтів рекурсивної та нерекурсивної частини ЛДС.

2. Сформувати відліки синусоїдального сигналу частоти 10 Гц тривалістю 1 сек. амплітуди 1 В, дискретизованого з частотою 256 Гц. Розрахувати реакцію системи на отриманий сигнал (функція filter) для двох випадків:

2.1. нульові початкові умови;

2.2. випадкові початкові умови (скористатися функцією rand).

Побудувати графіки вхідного та вихідного сигналів в одному вікні, позначивши точки графіку, що відповідають відлікам, та огинаючі графіків (налаштувати функцію plot). Побудувати в окремому вікні перші 100 мс вхідного та вихідного сигналу. Зробити висновки щодо вигляду вихідного сигналу відносно вхідного (форма, амплітуда, спотворення, підсилення).

clc

clear all

close all

a=[1 -0.0462 -0.0071 0 0 -0.0333];

b=[0.6 -0.45 0 -0.1667 0.3 -0.05];

Fs=256;

T=1;

t=0:1/Fs:T;

len=max(length(a),length(b))-1;

is=sin(2*pi*10*t);

os = filter(b,a,is);

osr = filter(b,a,is,rand(1,len));

figure

plot(t,is,'.-',t,os,'.-',t,osr,'.-');

grid on;

xlim ([0 0.1]);

ylim ([-1.5 1.5]);

legend('<Вхідний сигнал>', '<Вихідний сигнал без запізнення>','<Вихідний сигнал із запізненням>')

xlabel('t,c');

ylabel('A,B');

figure

plot(t,is,'.-',t,os,'.-',t,osr,'.-');

grid on;

ylim ([-1.5 1.5]);

legend('<Вхідний сигнал>', '<Вихідний сигнал без запізнення>','<Вихідний сигнал із запізненням>')

xlabel('t,c');

ylabel('A,B');

Висновок: вхідний та вихідний сигнал – синусоїдальні, мають однаковий період, проте вихідний сигнал має спотворення на початку. Вихідні сигнали (з запізненням та без) різняться лише протягом перших 40 мс, далі вони співпадають. Вхідний сигнал послаблюється. Різниця фаз майже непомітна (найімовірніше, вона становить лише декілька градусів).

3. Написати програму для визначення коефіцієнту передачі напруги ЛДС на частоті 10 Гц, а також різницю фаз між вихідним і вхідним сигналом.

clc

clear all

close all

a=[1 -0.0462 -0.0071 0 0 -0.0333];

b=[0.6 -0.45 0 -0.1667 0.3 -0.05];

Fs=256;

T=1;

t=0:1/Fs:T;

len=max(length(a),length(b))-1;

is=sin(2*pi*10*t);

os = filter(b,a,is);

osr = filter(b,a,is,rand(1,len));

[is_max, N]=findpeaks(abs(is));

[os_max, N1]=findpeaks(abs(os));

delta_t=t(N(7))-t(N1(7));

K_u = os_max(7)/is_max(7);

disp(['Різниця фаз ',num2str(delta_t)]);

disp(['Коефіціент підсилення ',num2str(K_u)])

Різниця фаз 0.050781

Коефіціент підсилення 0.20318

4. Сформувати два синусоїдальних сигнали частоти 3 та 20 Гц тривалістю 1 с. Проілюструвати властивість адитивності системи, визначивши реакцію системи спочатку на кожний з сигналів окремо, а потім на суму цих сигналів. Проілюструвати властивість однорідності системи. Навести необхідні графіки.

clc

clear all

close all

a=[1 -0.0462 -0.0071 0 0 -0.0333];

b=[0.6 -0.45 0 -0.1667 0.3 -0.05];

Fs=256;

T=1;

t=0:1/Fs:T;

is1=sin(2*pi*3*t);

is2=sin(2*pi*20*t);

os1=filter(b,a,is1);

os2=filter(b,a,is2);

os3=filter(b,a,is1 + is2);

os4=filter(b,a,is1*3);

os5=3*filter(b,a,is1);

subplot(2,1,1);

plot (t,os3);

xlabel('t,c');

ylabel('А,B');

title('Реакція ЛДС на суму двох сигналів');

subplot(2,1,2);

plot (t,os1+os2);

xlabel('t,c');

ylabel('А,B');

title('Сума реакцій ЛДС на два сигнали');

figure

subplot(3,1,1);

plot (t,os1);

xlabel('t,c');

ylabel('А,B');

title('Вхідний сигнал');

subplot(3,1,2);

plot (t,os4);

xlabel('t,c');

ylabel('А,B');

title('Реакція ЛДС на сигнал втричі більшої амплітуди ');

subplot(3,1,3);

plot(t,os5);

xlabel('t,c');

ylabel('А,B');

title('Реакція системи на сигнал, помножена на три');

5. Розрахувати за допомогою функції filter перші 30 відліків імпульсної характеристики системи, подавши на вхід системи одиничний імпульс (при нульових початкових умовах). Побудувати графіки вхідного та вихідного сигналу (функція stem).

clc

clear all

close all

a=[1 -0.0462 -0.0071 0 0 -0.0333];

b=[0.6 -0.45 0 -0.1667 0.3 -0.05];

t=0:29;

imp=zeros(1,30);

imp(1,1)=1;

os=filter(b,a,imp);

subplot(2,1,1);

stem (t,imp);

xlabel('n');

ylabel('А,B');

title('Вхідний сигнал (одиничний імпульс)');

subplot(2,1,2);

stem (t,os);

xlabel('n');

ylabel('А,B');

title('Вихідний сигнал (імпульсна харктеристика)');

6. Розрахувати 30 відліків імпульсної характеристики системи по коефіцієнтам різницевих рівнянь з використанням функції impz. Порівняти результати з результатами п. 5, побудувати графіки, зробити висновки.

clc

clear all

close all

a=[1 -0.0462 -0.0071 0 0 -0.0333];

b=[0.6 -0.45 0 -0.1667 0.3 -0.05];

imp=impz(b,a,30);

stem (imp);

xlabel('n');

ylabel('А,B');

title('Вихідний сигнал (імпульсна харктеристика)');

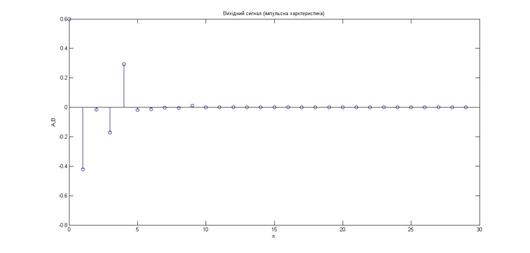
Імпульсні характеристики, знайдені в пунктах 5 і 6 співпадають, з чого можна зробити висновки, що ми можемо знаходити імпульсну характеристику двома способами.

Дата добавления: 2015-10-24