Розв'язання нормальних рівнянь

Відомо, що системи лінійних рівнянь можуть бути представлені і перетворені з використанням математичного апарату лінійної алгебри.

Використаємо приклад|зразок| системи параметричних лінійних рівнянь (10.8), приведений в попередньому підрозділі і покажемо їх матричне представлення.|виставу| Позначимо матрицю коефіцієнтів a розміром

,

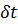матрицю-стовпець Δ розміром невідомих поправок , , , …, , яка є вектором поправок до найближчих значень параметрів , , ,…,

,

матрицю-стовпець L розміром вільних членів або вектором вільних членів системи рівнянь

l ,

і матрицю-стовпець v розміром або вектор поправок до результатів вимірів

.

Запроваджені позначення системи лінійних рівнянь (10.8) можна записати в матричній формі:

або у скороченому виді:

. (10.11)

Досліджуємо отримане матричне рівняння. Для цього виконаємо операцію транспонування матриці А і кожен член рівняння (10.11) помножимо на матрицю , отримаємо

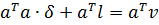. (10.12)

Розглянемо|розглядуватимемо| окремо в отриманому|одержувати| матричному рівнянні добутки , і .

Запишемо кожен елемент отриманої|одержувати| матриці в символах К.Ф. Гауса:

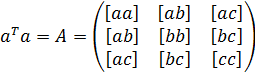, (10.13)

тобто отримана|одержувати| матриця коефіцієнтів нормальних рівнянь (10.10).

Розглянемо|розглядуватимемо| добуток матриці

, (10.14)

тобто отримана|одержувати| матриця-стовпець вільних членів нормальних рівнянь (10.10).

Знайдемо добуток матриці

. (10.15)

Тут елементи матриці Т можна прирівняти до нуля, тобто

, , , (10.16)

тому що беручи до уваги вирази (10.13) і (10.14) і порівнюючи рівняння (10.12) в матричній формі із системою рівнянь (10.10) приходимо до висновку, що їх ліві частини рівні. Отже, їх праві частини також мають бути рівні.

Беручи до уваги зроблені вище перетворення систему нормальних рівнянь запишемо у виді:

. (10.17)

Враховуючи, що матриця А є особливою, оскільки її визначник дорівнює нулю, а між рядками і стовпцями існує лінійна залежність, то для вирішення матричного рівняння (10.17) необхідно і достатньо помножити його зліва на матрицю зворотну матриці А. В результаті отримаємо матричне рівняння:

. (10.18)

Отримана матриця-стовпець δ поправок до виміряних величин v.

Приведені вище математичні перетворення, дають підставу|основу| записати строгу|сувору| послідовність процедур, що забезпечують зрівнювання параметричним способом з використанням вихідних даних у вигляді матриць.

Процедура 1. Підготовка вихідних даних для зрівнювання.

Необхідно підрахувати кількість шуканих невідомих t, а також число незалежних вимірів n і визначити число надлишкових вимірів . Якщо , , то завдання зрівнювання виміряних величин не виникає.

Процедура 2. Визначення наближених значень невідомих , , ,…, з використанням тільки необхідних вимірів.

Процедура 3. Складання рівнянь поправок в загальному вигляді (10.2) і їх лінеаризація (10.7). Внаслідок виконання процедури отримуємо|одержуємо| коефіцієнти рівнянь поправок a, b, c,…, q.

Процедура 4. Обчислення вільних членів рівнянь поправок за формулами (10.6).

Процедура 5. Складання рівняння поправок в матричній формі (10.11). В результаті виконання процедури складаються матриці коефіцієнтів рівнянь поправок a розміром і матриця-стовпець вільних членів l розміром .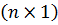

Процедура 6. Транспонування матриці a.

Процедура 7. Множення матричного рівняння (10.11) зліва на матрицю . Внаслідок виконання процедури отримуємо|одержуємо| систему нормальних рівнянь (10.10) представлену|уявляти| в матричній формі (10.17).

Процедура 8. Обернення матриці коефіцієнтів нормальних рівнянь А і отримання матриці . Розмір матриць складає .

Процедура 9. Множення рівняння (10.17) зліва на матрицю . В результаті виконання процедури отримуємо матрицю-стовпець поправок Δ розміром .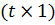

Процедура 10. Обчислення зрівняних значень невідомих x, у,…, t за формулами (10.3).

Процедура 11. Підстановка матриці-стовпця δ в рівняння (10.11), а також множення і підсумовування матриць. В наслідок виконання процедури отримуємо матрицю-стовпець поправок до зміряних величин v розміром (n . Обчислюються зрівняні значення .

Процедура 12. Оцінка точності отриманих в результаті зрівнювання невідомих величин x, у,…, t.

Таким чином, параметричний спосіб має на увазі обчислення поправок не до виміряних величин, а до деяких наближених значень (параметрів), тобто до кінцевих результатів зрівнювання, якими в геодезичних мережах є координати або висоти пунктів, і безпосереднє отримання найймовірніших значень параметрів, минувши найймовірніші значення виміряних елементів мережі.

Наведено як на основі лінійної алгебри, а саме матричних представлень|вистав|, а також операцій над ними можна розв’язувати нормальні рівняння зрівнювання геодезичних вимірів параметричним способом. Приведена строга|сувора| послідовність математичних процедур, що забезпечують оперативне вирішення практичних задач зрівнювання.

---

Дата добавления: 2015-10-29