Сутність методу найменших квадратів і обґрунтування

його використання у зрівнюванні геодезичних побудов|шикувань|

Метод найменших квадратів є одним з методів регресійного аналізу і призначений для оцінки невідомих величин за результатами вимірів, що містять випадкові похибки. Він застосовується також для наближеного представлення заданої функції іншими (простішими) функціями і часто виявляється корисним при обробці спостережень.

З метою збільшення точності результатів вимірів в геодезії виміри шуканої фізичної величини здійснюються багато разів і за остаточний результат приймають арифметичну середину із всіх окремих вимірів. Властивості арифметичної середини мають стохастичну|самодифузія| природу і розглянуті|розглядувати| в п. 5.1. Враховуючи властивості арифметичної середини легко навести, що сума квадратів відхилень окремих вимірів від арифметичної середини буде менша, ніж сума квадратів відхилень окремих вимірів від якої іншої величини. Отже, правило обчислення|підрахунку| арифметичної середини є простим випадком методу найменших квадратів.

Суть вирішення невизначених|неозначених| систем рівнянь, що описують деяку геодезичну побудову|шикування| полягає в тому, що на них накладаються умови мінімізації

для нерівноточних вимірів, де – ваги вимірів – поправка вимірів. У разі рівноточних вимірів формула (9.3) матиме вигляд:

Розглянемо|розглядуватимемо| рішення задачі зрівнювання з використанням методу найменших квадратів на прикладі|зразку| системи рівнянь (9.2). Представимо цю систему рівнянь у виді:

;

де . Підставимо отримані співвідношення 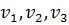у формулу (9.3) отримаємо функцію

.

З курсу математичного аналізу відомо, що однією з операцій дослідження монотонної функції є її диференціювання або взяття першої похідної для знаходження в ній локальних екстремумів (мінімуму і максимуму). Тому для визначення мінімуму отриманої функції візьмемо першу похідну по змінній і прирівняємо її до нуля (умова існування локального екстремуму). Отримаємо:

.

Перетворимо отриманий вираз так, щоб шукана величина Н залишилась в лівій частині виразу. Для цього розкриємо дужки і виконаємо елементарні перетворення, отримаємо:

,

.

Розділимо праву і ліву частини рівняння на отримаємо:

Вираз (9.4) є загальною|спільною| арифметичною серединою, властивості якої розглянуті в п.п. 6.3.

Для того, щоб визначити який із локальних екстремумів знайдений (мінімум або максимум) продовжимо досліджувати функцію визначаючи її опуклість або увігнутість. Для цього візьмемо другу похідну від отриманої|одержувати| функції. Позначимо

Вираз (9.4) матиме вигляд:

тоді Якщо друга похідна функції більше нуля, то локальний екстремум функції є її мінімумом. Отже, справедливо записати:

Отримано|одержувати| єдине рішення системи рівнянь (9.2). При цьому воно виявилося виразом для обчислення|підрахунку| загальної|спільної| арифметичної середини, що підтверджує єдність методу найменших квадратів і методу обчислення|підрахунку| арифметичної середини.

Із системи лінійних рівнянь (9.2) і отриманої|одержувати| загальної|спільної| арифметичної середини виходить, що її розв'язання відповідатиме мінімуму|мінімум-ареалу| функції (9.3) і відповідно до мінімуму|мінімум-ареалу| емпіричної середньої квадратичної похибки| одиниці ваги, яка характеризує точність нерівноточних| вимірів і обчислюється за формулою (6.31). Отже, вагу шуканої величини можна визначити за формулою

де с |із| – довільна позитивна постійна.

Очевидно, що при будь-яких значеннях с і [ p ] вага вимірюваної величини p_H буде максимальною. Тому рішення, знайдене методом найменших квадратів відповідає найбільшій вазі шуканої величини.

Виникає питання, наскільки принцип найменших квадратів відповідає природі накопичення похибок вимірів і чи стають значення виміряних|виміряти| величин, виправлені поправками, знайденими методом найменших квадратів, ближче до дійсних значень?

Відповімо на це питання висловлюваннями відомого німецького геодезиста Ф.Р. Гельмерта, який ще в XIX ст. зробив наступні|слідуючі| роз'яснення:

1. Якщо результати вимірів містять|утримують| лише випадкові похибки, що підкоряються нормальному закону розподілу, то значення невідомих, отримані|одержувати| методом найменших квадратів будуть найймовірнішими| значеннями невідомих і володітимуть найменшою середньою квадратичною похибкою|.

2. Якщо результати вимірів містять похибки, що володіють тільки властивостями компенсації (див. п.п.2.5, властивості обмеженості, незалежності, розсіювання) значення невідомих, хоча і матимуть найбільшу вагу, але не можуть вважатися за найймовірніші значення невідомих.

3. Якщо ж результати вимірів окрім випадкових, суттєво обтяжені систематичними похибками, то зрівнювання вимірів методом найменших квадратів дасть, як завжди однозначне розв'язання, та знайдені значення не будуть найймовірнішими| і не володітимуть найбільшою вагою.

Таким чином, невизначеність систем рівнянь, що описують процеси вимірів (див. п.п. 9.2), а також роз'яснення, зроблені Ф.Р. Гельмертом зумовило появи двох способів зрівнювання геодезичних побудов – параметричний спосіб, що застосовується у випадку, якщо невизначеність системи рівнянь носить перевизначений характер і спосіб зрівнювання виміряних величин, зв'язаних деякими умовами, якщо система рівнянь є недовизначеною. Останній спосіб ще називається корелатним.

Дата добавления: 2015-10-29