Загальна|спільна| арифметична середина і її властивості

Якщо l₁, l₂,…, l_n – незалежні результати вимірів однієї і тієї ж величини Х, відносна точність яких характеризується відповідно вагами p₁, p₂,…, p_n (вимірювання нерівноточні) то за якнайкраще наближені до величини Х приймають загальну арифметичну середину

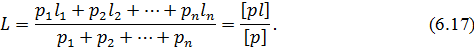
Величину L часто називають середньою зваженою.

Отриману|одержувати| формулу (6.17) можна застосовувати лише тоді, коли окремі результати вимірів можливо порівнювати|вимірів| і вони мають величини одного порядку|ладу|. Не можна усереднювати результати, отримані|одержувати| за умов вимірів|вимірів|, що суттєво відрізняться, наприклад, не можна усереднювати довжину лінії, виміряну|виміряти| один раз звичайною|звичною| рулеткою, а другий раз світлодальноміром|, або величину кута|рогу|, виміряного|виміряти| один раз технічним теодолітом, а другий раз високоточним теодолітом. Виходячи з вищевикладеного випливає, що на ваги у формулі (6.17) мають бути накладені обмежувальні умови, які можна виразити|виказувати| нерівністю

де c₁, c₂ – деякі позитивні постійні.

За аналогією з математичними побудовами|шикуваннями| виконаними|проробити| в п.п.5.1 розглянемо|розглядуватимемо| основні властивості загальної|спільної| арифметичної середини незалежних нерівноточних| результатів вимірів|вимірів|.

Властивості загальної|спільної| арифметичної середини

Властивість 1. Вага загальної арифметичної середини незалежних нерівнаточних результатів вимірів дорівнює сумі вагів цих вимірів.

Для математичного обґрунтування цього твердження представимо |затвердження| формулу (6.17) |уявлятимемо| у вигляді

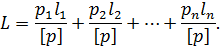
Розглядаючи L як функцію незалежних змінних l₁, l₂,…, l_n для визначення її ваги, знайдемо частинні похідні

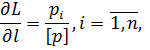
і підставимо їх до формули (6.6). У результаті отримаємо|одержуватимемо| наступне|слідуюче| співвідношення

Після|потім| скорочень і перетворення отриманої|одержувати| формули, маємо

що формально демонструє вірність|вмісту| властивості 1. Відповідно стандарт загальної|спільної| арифметичної середини, враховуючи формулу (6.8), буде рівний

Властивість 2. Якщо загальна арифметична середина отримане з результатів вимірів, вільних від систематичних похибок, то і сама вона не містить систематичної похибки.

Ця властивість, аналогічно третій властивості простої арифметичної середини, яка розглядалася|розглядувало| для ряду рівноточних|лави| вимірів|вимірів| в п.п.5.1. Тому справедливим є запис

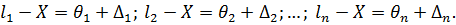
Помноживши кожну з цих рівностей на відповідну вагу , та склавши почленно і розділивши на [ p ] отримаємо

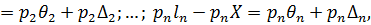
Права частина отриманої рівності складається з двох частин, які відповідають систематичній і випадковій похибкам загальної арифметичної середини. Звідси витікає, що якщо θ₁=θ₂=…=θ_n дорівнює нулю, то і [ pθ ] дорівнюватиме нулю, що і доводить сформульовану вище властивість.

Властивість 3. Якщо результати нерівноточних вимірів вільні від систематичних похибок, то їх загальна арифметична середина при збільшенні кількості вимірів наближається до істинного значення вимірюваної величини.

За аналогією з першою властивістю простої арифметичної середини для ряду рівноточних|лави| | результатів вимірів|вимірів| запишемо

На підставі обмежувальних умов на вимірювання (6.18) запишемо наступні нерівності c₁<p₁; c₁<p₂;…; c₁<p_n. Підсумуємо праві і ліві їх частини і отримаємо нову нерівність 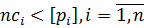. Звідки можна зробити висновок, що за n→∞ має місце границя

З отриманого виразу (6.22) і формули (6.20) виходить, що стандарт σ_L наближатиметься до нуля, тобто при n→∞

Це означає, що загальна|спільна| арифметична середина L наближатиметься до постійної величини, а оскільки|тому що| постійна величина не може містити|утримувати| систематичної похибки, то вона має дорівнювати вимірюваній величині Х.

На підставі третьої і другої властивості можна зробити висновок|укладення|, що за відсутності систематичних похибок загальна|спільна| арифметична середина L є|з'являється| спроможною і незміщеною оцінкою Х.

Властивість 4. Сума добутків відхилень результатів вимірів від загальної арифметичної середини

на відповідні їх ваги дорівнює нулю|нуль-індикатору|, тобто

Помножимо почленно кожний вираз із системи рівнянь (6.24) на відповідні ваги і, підсумувавши отриману|одержувати| у такий спосіб|в такий спосіб| рівність, матимемо

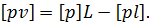
Враховуючи формулу для знаходження загальної арифметичної середини (6.17) підставляючи її до отриманого виразу і перетворюючи, матимемо

Підставляючи до отриманої формули вираз (6.25) отримаємо , що і потрібно було довести.

Залишається обґрунтувати, що з|із| усіх можливих функцій, отриманих|одержувати| в результаті нерівноточних|унаслідок|| вимірів|вимірів| цю властивіст має тільки|лише| загальне|спільна| арифметичне середнє. Для цього візьмемо відмінну від (6.24) деяку функцію у |біля| і запишемо для неї систему рівнянь:

Віднімаючи від|із| формули (6.26) вираз|вираження| (6.24), отримаємо|одержуватимемо| різницю відхилень

Помножимо кожну з рівностей на відповідні ваги , а потім підсумуємо почленно і отримаємо формулу , яку, враховуючи (6.25), можна перетворити на співвідношення вигляду 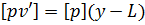. Звідси витікає, що буде дорівнювати нулю, тоді і тільки тоді, коли y=L що і потрібно було довести.

Властивість 5. Сума добутків ваг на квадрати відхилень від загальної арифметичної середини завжди менша суми добутків ваг на квадрати

відхилень від будь-якої іншої функції тих же результатів вимірів, тобто

що відповідає нерівності

Для доказу отриманої|одержувати| нерівності перетворимо формулу (6.27) до вигляду

|виду|

Піднесемо ліві і праві частини|частки| цієї рівності до квадрату і, привівши їх у відповідність з|із| формулами скороченого множення для многочленів, отримаємо|одержуватимемо|:

…

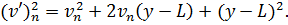
Потім помножимо ліві і праві частини отриманих рівнянь на відповідні ваги , отримані вирази почлено складемо. У результаті отримаємо формулу яка з урахуванням рівності (6.25) набере вигляду . Звідки випливає очевидна нерівність (6.29), що і підтверджує справедливість формулювання п'ятої властивості загальної арифметичної середини результатів нерівноточных вимірів.

Таким чином, враховуючи окремі математичні формули|шикування| знаходження простої арифметичної середини для рівноточних| вимірів|вимірів|, розглянуті|розглядувати| властивості загальної|спільної| арифметичної середини однієї з основних характеристик оцінювання точності нерівноточних| геодезичних вимірів|вимірів|.

Знання властивостей загальної|спільної| арифметичної середини дозволяє правильно і коректно організувати математичні обчислення|підрахунки| в процесі обробки нерівноточних| геодезичних вимірів|вимірів|.

Дата добавления: 2015-10-29