Завдання Д-4. Загальне рівняння динаміки

Умова завдання. Механічна система складається з однорідних ступінчастих шківів 1 і 2, обмотаних нерозтяжними нитками, вантажів 3 – 6, прикріплених до цих ниток, та невагомого блока (рис. Д4.0 – Д4.9, табл. Д4). Система рухається у вертикальній площині під дією сил ваги та пари сил з моментом 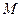, прикладеної до одного з шківів. Радіуси ступенів шківа 1 дорівнюють: 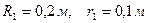, а шківа 2 – ; радіуси інерції відносно осей обертання дорівнюють відповідно та . Вага тіл задана в табл. Д4. Вантажі, вага яких дорівнює нулю, на рисунку не зображати, шківи 1 і 2 зображати завжди.

Визначити. Прискорення вантажу, що має найбільшу вагу, нехтуючи тертям.

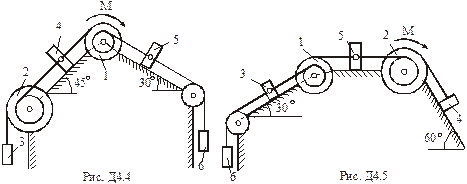
Табл. Д4

№ умови		,	,	,	,	,

Теоретичне обґрунтування: [5] § 137 – 141; [6] Розд.III. Гл.6. § 1 – 3, 8;

[8] § 112, 117, 118; [9]; [13]; [15]; [17].

Методичні вказівки. Завдання Д-4 на тему «Загальне рівняння динаміки». Для систем з геометричними, стаціонарними ідеальними в’язями означене рівняння має вигляд:

, (Д4.1)

де сума можливих робіт активних сил, що діють на систему; сума можливих робіт сил інерції.

(У наведених вище сумах під можливою роботою розуміється робота сил на якомусь можливому переміщенні системи).

Сили інерції точок, з яких складаються тверді тіла, можна звести до головного вектора та головного моменту сил інерції відносно вибраного центру зведення (в динаміці за центр зведення беруть точку - центр мас тіла). Для тіл, що виконують поступальний, обертальний або плоский рухи головний вектор і головний момент сил інерції визначаються за правилами.

Для тіла, що виконує поступальний рух:

- головний вектор , головний момент , (Д4.2)

де маса тіла, прискорення центру мас тіла.

Головний вектор сил інерції та прискорення центру мас спрямовані протилежно.

Для тіла, що виконує обертальний рух навколо нерухомої центральної осі:

- головний вектор 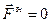, головний момент 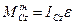, (Д4.3)

де осьовий момент інерції, 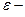кутове прискорення тіла.

Головний момент сил інерції та кутове прискорення спрямовані протилежно.

Для тіла, що виконує плоский рух:

- головний вектор , головний момент 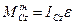, (Д4.4)

Головний вектор і головний момент сил інерції спрямовані протилежно відповідним прискоренням.

Приклад Д-4

Механічна система (рис. Д4.а) складається із з’єднаних нерозтяжними нитками блока 1 радіуса і ступінчастого шківа 2 (радіуси ступіней і 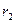, радіус інерції відносно осі обертання ), а також вантажів 3 і 4, прикріплених до цих ниток. Система рухається у вертикальній площині під дією сил ваги та пари сил з моментом 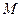, прикладеної до блока 1.

Дано:

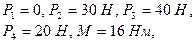
Визначити: прискорення вантажу 3, нехтуючи тертям.

Дата добавления: 2015-10-31