
Читайте также:
|
Умова завдання. Механічна система складається із вантажів 1 і 2 (коефіцієнт тертя вантажів з площиною 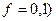 , циліндричного однорідного котка 3 та ступінчастих шківів 4 і 5 з радіусами ступіней
, циліндричного однорідного котка 3 та ступінчастих шківів 4 і 5 з радіусами ступіней 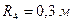 ,
, 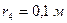 ,
, 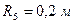 ,
, 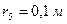 (масу кожного шківа вважати розподіленою по зовнішньому ободу) (рис.Д3.0– Д3.9, табл.Д3). Якщо маса тіла 2 m2 = 0, груз 2 на рисунку не зображати; шківи 4 і 5 та вантаж 1 завжди входять в систему. Тіла зв'язані між собою нерозтяжними нитками, намотаними на шківи; ділянки ниток паралельні відповідним площинам. Коток 3 котиться без ковзання. Точка
(масу кожного шківа вважати розподіленою по зовнішньому ободу) (рис.Д3.0– Д3.9, табл.Д3). Якщо маса тіла 2 m2 = 0, груз 2 на рисунку не зображати; шківи 4 і 5 та вантаж 1 завжди входять в систему. Тіла зв'язані між собою нерозтяжними нитками, намотаними на шківи; ділянки ниток паралельні відповідним площинам. Коток 3 котиться без ковзання. Точка 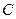 є центром мас котка 3.
є центром мас котка 3.
Під дією сили F =f(s), що залежить від переміщення вантажу 1, система починає рухатись. В початковий момент часу система знаходилась в спокої. На шківи 4 та 5 діють постійні за величиною моменти опору, що дорівнюють відповідно 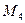 та
та 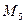 .
.
Визначити. В момент часу, коли переміщення точки прикладання сили 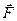 дорівнює
дорівнює 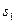 , визначити указані в стовпцях «Знайти» (табл.Д3) швидкості.
, визначити указані в стовпцях «Знайти» (табл.Д3) швидкості.
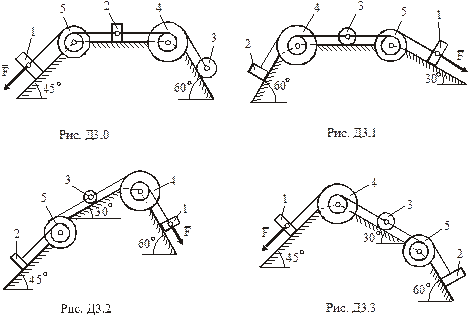
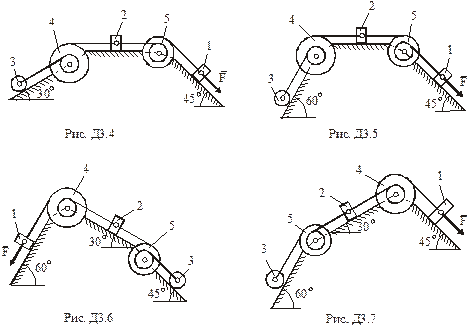

Табл.Д3.
| № умови | 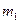 , кг , кг
| 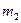 , кг , кг
| 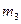 , кг , кг
| 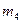 , кг , кг
| 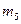 , кг , кг
| 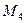 , Н·м , Н·м
| 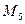 , Н·м , Н·м
| 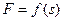 , Н , Н
| 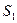 , м , м
| Визна-чити |
| 0,8 | 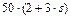
| 1,0 | 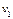
| |||||||
| 0,6 | 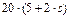
| 1,2 | 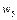
| |||||||
| 0,4 | 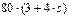
| 0,8 | 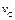
| |||||||
| 0,3 | 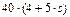
| 0,6 | 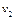
| |||||||
| 0,6 | 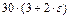
| 1,4 | 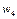
| |||||||
| 0,9 | 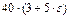
| 1,6 | 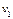
| |||||||
| 0,8 | 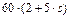
| 1,0 | 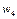
| |||||||
| 0,6 | 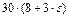
| 0,8 | 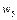
| |||||||
| 0,3 | 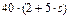
| 1,6 | 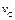
| |||||||
| 0,4 | 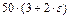
| 1,4 | 
|
Теоретичне обґрунтування: [5] § 121 – 124; [6] Розд.III. Гл.4. § 5 – 7;
[8] § 58, 61, 65 – 69; [9]; [13]; [14]; [15]; [16].
Методичні вказівки. Завдання Д-3 на тему «Теорема про зміну кінетичної енергії механічної системи в інтегральній формі».
Для незмінних механічних систем (тобто 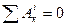 ) теорема має вид:
) теорема має вид:
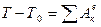 , (Д3.1)
, (Д3.1)
де Т - кінетична енергія системи в кінцевому положенні;
Т0 - кінетична енергія системи в початковому положенні;
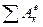 - сума робіт зовнішніх сил, діючих на систему на заданому її переміщенні;
- сума робіт зовнішніх сил, діючих на систему на заданому її переміщенні;
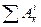 - сума робіт внутрішніх сил, діючих в системі на заданому її переміщенні.
- сума робіт внутрішніх сил, діючих в системі на заданому її переміщенні.
Кінетична енергія системи дорівнює сумі кінетичних енергій тіл системи, тобто:
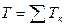 (Д3.2)
(Д3.2)
В залежності від того, який рух виконує тверде тіло, кінетична енергія визначається:
1) при поступальному русі 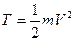 , (Д3.3)
, (Д3.3)
де m - маса тіла; V – швидкість тіла.
2) при обертальному русі тіла навколо нерухомої осі z
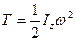 , (Д3.4)
, (Д3.4)
де Iz - осьовий момент інерції тіла відносно осі z;
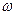 - кутова швидкість тіла.
- кутова швидкість тіла.
3) при плоскому русі в площині Сxy
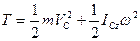 , (Д3.5)
, (Д3.5)
де m – маса тіла; VC – швидкість центру мас тіла; ICz - осьовий момент інерції тіла відносно осі Сz; 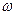 - кутова швидкість тіла.
- кутова швидкість тіла.
Момент інерції однорідного котка: 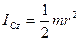 .
.
Момент інерції кільця радіуса R: 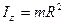 .
.
Робота змінної сили F =f(s):
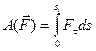 , (Д3.6)
, (Д3.6)
де 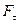 - проекція сили на напрямок переміщення точки прикладення сили.
- проекція сили на напрямок переміщення точки прикладення сили.
Робота постійної сили 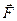 :
:
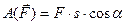 , (Д3.7)
, (Д3.7)
де 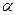 - кут між силою
- кут між силою 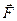 і напрямком переміщення точки прикладення сили.
і напрямком переміщення точки прикладення сили.
Робота пари сил з моментом 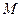 :
:
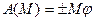 , (Д3.8)
, (Д3.8)
де 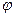 - кут повороту тіла. Знак „+” беремо, якщо момент М і кут
- кут повороту тіла. Знак „+” беремо, якщо момент М і кут 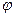 однаково спрямовані, та „ – ”, якщо вони спрямовані протилежно.
однаково спрямовані, та „ – ”, якщо вони спрямовані протилежно.
Приклад Д-3
Механічна система (рис.Д3. а) складається з вантажу 1, ступінчастого шківа 2 з радіусами ступіней R2 і r2 (маса шківа рівномірно розподілена по зовнішньому ободу) та однорідного циліндричного котка 3. Коефіцієнт тертя між вантажем та площиною f. Тіла зв’язані між собою нерозтяжними нитками, намотаними на шків 2.
Під дією сили F =f(s), що залежить від переміщення вантажу 1, система починає рухатись із стану спокою. При русі на шків діє постійний момент сил опору М2.
 Дано: m1 = 4 кг, m2 = 10 кг, m3 = 8 кг,
Дано: m1 = 4 кг, m2 = 10 кг, m3 = 8 кг,
R2 = 0,2 м, r2 = 0,1 м, f = 0,2,
M = 0,6 Н м, F = 200(5+ 2s) H,
S1 =0,2 м.
Визначити: швидкість VC центра мас котка 3, коли переміщення вантажу 1 буде дорівнювати S1.
Розв’язування.
1. Розглянемо рух незмінної механічної системи, що складається з тіл 1, 2, 3, з’єднаних між собою за допомогою ниток (рис.Д3.б). Зобразимо всі діючи на систему зовнішні сили: активні 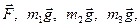 момент сил опору
момент сил опору 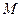 , реакції
, реакції 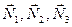 , сили тертя ковзання
, сили тертя ковзання 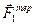 та тертя кочення
та тертя кочення 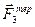 .
.
Для визначення VC використаємо теорему про зміну кінетичної енергії
механічної системи

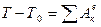 , (1)
, (1)
2. Визначимо 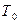 та
та 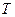 .
.
Кінетична енергія системи дорівнює сумі кінетичних енергій окремих тіл системи. Якщо в початковий момент часу система знаходилась у стані спокою, маємо:
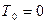
Для кінцевого положення системи, враховуючи, що тіло 1 виконує поступальний рух, тіло 2 – обертається навколо нерухомої осі, а тіло 3 – рухається в площині, маємо:
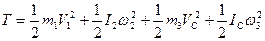 (2)
(2)
Момент інерції ступінчастого шківа, маса якого розподілена по його зовнішньому ободу, дорівнює:
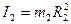 (3)
(3)
Момент інерції однорідного котка 3, визначається за формулою:
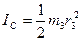 (4)
(4)
Виразимо всі швидкості через невідому швидкість центра мас котка 3 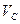 :
:
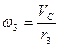 ,
, 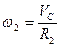 ,
, 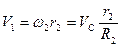 (5) Підставимо формули (3) – (5) у вираз (2) і отримаємо
(5) Підставимо формули (3) – (5) у вираз (2) і отримаємо
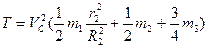 (6)
(6)
4. Тепер знайдемо суму робіт всіх діючих зовнішніх сил при переміщенні, яке буде мати система, коли вантаж 1 пройде шлях S1.
Робота сили 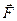 дорівнює:
дорівнює:
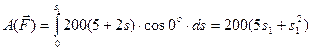
Роботи сили ваги 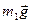 та реакції
та реакції 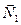 дорівнюють нулю, бо кут між цими силами та переміщенням S1 складає 900.
дорівнюють нулю, бо кут між цими силами та переміщенням S1 складає 900.
Між силою тертя ковзання 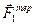 та переміщенням S1 кут 1800, тому A(
та переміщенням S1 кут 1800, тому A(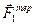 ) =
) = 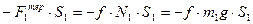 ,
,
де 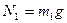 , бо вантаж знаходиться на горизонтальній площині.
, бо вантаж знаходиться на горизонтальній площині.
Момент М спрямований протилежно напрямку 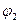 , тому його робота дорівнює
, тому його робота дорівнює
A(M) 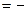 M
M 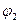
Роботи сили ваги 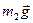 та реакції
та реакції 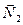 дорівнюють нулю, бо точка прикладання цих сил нерухома.
дорівнюють нулю, бо точка прикладання цих сил нерухома.
Робота сили ваги 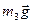 (кут між нею та переміщенням центра ваги катка
(кут між нею та переміщенням центра ваги катка 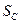 дорівнює 1500):
дорівнює 1500):
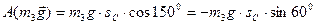 .
.
Точка прикладання сил 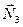 та
та 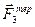 є миттєвим центром швидкостей, тому робота цих сил дорівнює нулю.
є миттєвим центром швидкостей, тому робота цих сил дорівнює нулю.
Таким чином, сума робіт діючих зовнішніх сил, що діють на систему на заданому її переміщенні:
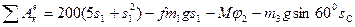 (7)
(7)
Виразимо всі переміщення через переміщення вантажу 1 S1:
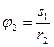 ;
; 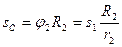 (8)
(8)
Підставимо (6) та (7) з врахуванням (8) в вираз теореми (1) та отримаємо:
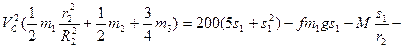
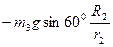 (9)
(9)
Підставимо чисельні значення та знайдемо швидкість центру ваги котка 3 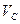
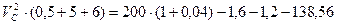
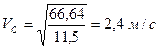
Відповідь: 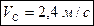
Дата добавления: 2015-10-31; просмотров: 180 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Завдання Д-2. Динамічні рівняння руху тіл | | | Завдання Д-4. Загальне рівняння динаміки |