Завдання К-1. Кінематика точки

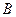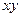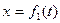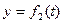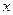Умова завдання. Точка рухається в площині (рис.К1.0-К1.9, табл.К1; траєкторія точки на рисунках показана умовно). Закон руху точки заданий рівняннями: , , де і 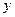виражені в сантиметрах, - у секундах.

Визначити. 1) Траєкторію руху точки; 2) для моменту часу 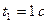визначити положення точки на траєкторії, її швидкість та прискорення, а також дотичне і нормальне прискорення і радіус кривизни у відповідній точці траєкторії.

Залежність 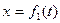зазначена на рисунках (рис.К1.0-К1.9), а залежність 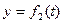дана в табл.К1 (для рис.К1.0-К1.2 у стовпці 2, для рис.К1.3-К1.6 у стовпці 3, для рис.К1.7-К1.9 у стовпці 4).

Усі знайдені величини зобразити на рисунку.

Табл.К1

Номер умови
Рис.0-2	Рис.3-6	Рис.7-9

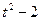
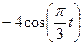
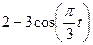
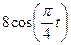
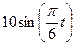
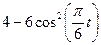
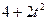
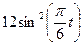
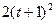
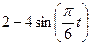
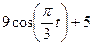
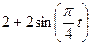
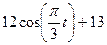
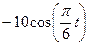
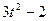
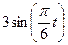
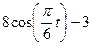
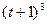
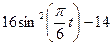
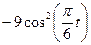
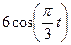
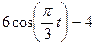
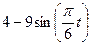
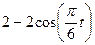
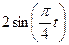
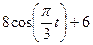
Теоретичне обґрунтування: [5] §36-46, [6] Разд.II, Гл. 1§.1-5, [7] Разд.2, гл.VII,§.62-65, гл.VIII, §66-68, гл.IX, § 70-77; [9]; [ 10].

Методичні вказівки. Завдання К-1 відноситься до задач кінематики точки. Тому задача зводиться до визначення траєкторії руху точки та її кінематичних характеристик (швидкості і прискорення).

Якщо рух точки відбувається у площині і заданий координатним способом, тобто 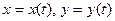, для визначення виду траєкторії необхідно виключити час з цих рівнянь і отримати залежність 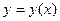.* Траєкторією руху точки є графічне відображення цієї залежності за умовою 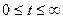. Розрахункове положення точки – це положення точки в момент часу .

У координатному способі швидкість 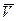точки визначають по формулах:

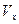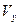де і - проекції вектора 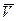швидкості точки на осі нерухомої декартової системи координат .

Аналогічно визначають прискорення:

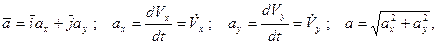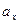де і 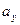- проекції вектора 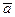прискорення точки на осі нерухомої декартової системи координат .

Кінематичні характеристики точки визначаються також через проекції на рухомі осі координат (осі природного тригранника). При цьому швидкість завжди буде спрямована уздовж дотичної до траєкторії осі 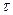. Вектор прискорення знаходять через його проекції на нормаль і дотичну :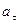

,

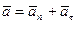де 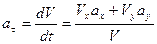і .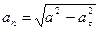

Варто підкреслити, що незалежно від способу розкладання вектора прискорення на складові, сума проекцій повинна давати той самий вектор 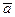, що також є показником правильності отриманого результату.

Приклад К-1

Рух точки відбувається в площині і заданий параметричними рівняннями:

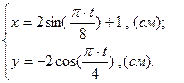(1)

Визначити:

1. Рівняння траєкторії руху точки. Зобразити траєкторію на рисунку.

2. Положення точки на траєкторії в момент часу 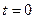і .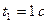

3. Швидкість точки в момент часу .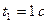

4. Прискорення точки в момент часу .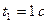

5. Дотичне і нормальне прискорення точки в момент часу .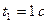

6. Радіус кривизни траєкторії точки в момент часу .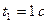

Усі знайдені величини зобразити на рисунку в масштабі.

Дата добавления: 2015-10-31