
|
Читайте также: |
1. Для визначення рівняння траєкторії точки виключимо параметр  із рівнянь руху (1). Ураховуючи, що час
із рівнянь руху (1). Ураховуючи, що час  входить в аргумент тригонометричних функцій, скористаємося формулою:
входить в аргумент тригонометричних функцій, скористаємося формулою:
 , тобто
, тобто  (2)
(2)
З рівнянь руху знаходимо вирази відповідних функцій і підставляємо в рівність (2)
 чи
чи 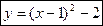 (3)
(3)
Рівняння параболи (3) є рівнянням траєкторії руху точки. Враховуючи, що
-1  та -1
та -1  , маємо обмеження для
, маємо обмеження для 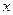 та
та 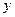 :
:
-1  та -2
та -2  , тобто траєкторією руху точки є частина параболи. Побудуємо траєкторію точки на рисунку К1.а з масштабним коефіцієнтом
, тобто траєкторією руху точки є частина параболи. Побудуємо траєкторію точки на рисунку К1.а з масштабним коефіцієнтом  .
.
2. Визначимо початкове положення точки і положення точки в момент часу 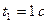 на траєкторії. Для цього підставимо в рівняння (1) час
на траєкторії. Для цього підставимо в рівняння (1) час  і
і  . Отримаємо:
. Отримаємо:
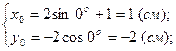 (4)
(4)
 (5)
(5)
Таким чином  (1;-2), а
(1;-2), а  (1,77; -1,41). Покажемо ці точки на траєкторії (рис.К1.а).
(1,77; -1,41). Покажемо ці точки на траєкторії (рис.К1.а).

3. Визначимо швидкість точки. Проекції швидкості в довільний момент часу дорівнюють:
 (6)
(6)
В момент часу 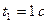

Модуль швидкості для моменту 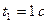 :
:
 .
.
Побудуємо вектор швидкості  точки
точки  по його складовим
по його складовим
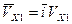 ,
,  , де
, де 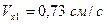 і
і  в масштабі
в масштабі  (рис.К1.а).
(рис.К1.а).
4. Визначимо прискорення точки. Проекції прискорення в довільний момент часу дорівнюють:
 (7)
(7)
У момент часу 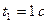 одержимо:
одержимо:

Модуль прискорення точки  :
:

Вектор 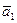 повного прискорення точки
повного прискорення точки  побудуємо по його складових
побудуємо по його складових  , де
, де  і
і  в масштабі
в масштабі  (рис.К1.б).
(рис.К1.б).
5. Визначимо дотичне і нормальне прискорення точки в момент часу 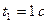 , використовуючи формули:
, використовуючи формули:

Побудуємо вектор 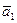 повного прискорення точки
повного прискорення точки  по проекціях
по проекціях  і
і 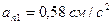 (рис.К1.б). Для зображення векторів використовуємо той же масштаб, тобто
(рис.К1.б). Для зображення векторів використовуємо той же масштаб, тобто  Значення дотичного прискорення
Значення дотичного прискорення  виявилося додатнім, тому відкладаємо його по осі М
виявилося додатнім, тому відкладаємо його по осі М 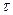 (дотичної до траєкторії) у напрямку вектора швидкості
(дотичної до траєкторії) у напрямку вектора швидкості  . Вектор нормального прискорення
. Вектор нормального прискорення  направимо перпендикулярно до осі М
направимо перпендикулярно до осі М 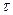 по нормалі М
по нормалі М  (вбік увігнутості траєкторії).
(вбік увігнутості траєкторії).
Збіг векторів повного прискорення при вирішенні задачі в нерухомій системі координат Оxy і рухомій системі координат М  говорить про правильність результату.
говорить про правильність результату.
6. Радіус кривизни траєкторії в точці  визначимо по формулі:
визначимо по формулі:

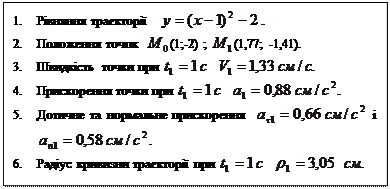 Відповідь.
Відповідь.
Дата добавления: 2015-10-31; просмотров: 137 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Завдання К-1. Кінематика точки | | | Завдання К-2. Кінематика простих рухів тіл |