Розв’язування. Механізм (рис.К2.а) є механічною системою з одним ступенем вільності

Механізм (рис.К2.а) є механічною системою з одним ступенем вільності. Тобто рух кожного з елементів пов’язаний з рухом інших елементів жорсткими кінематичними співвідношеннями. Тому, якщо рух одного з тіл задається, кінематичні характеристики інших тіл і їх точок фактично є визначеними. В умові даної задачі задається рух рейки 4.

1. Визначимо швидкості тіл механізму.

Знаючи закон поступального руху рейки 4, знайдемо її швидкість

. При .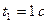

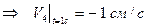Знак «-» указує на те, що в даний момент часу вектор швидкості спрямований протилежно додатному напрямку осі , тобто вгору (рис.К2.б).

Рейка 4 контактує без ковзання з внутрішнім ободом колеса 1. Враховуючи це, отримаємо рівняння зв’язку рухів тіл 1 і 4:

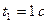. При одержимо .

Напрямок кутової швидкості залежить від напрямку швидкості рейки. У даному випадку спрямована проти руху годинникової стрілки.

Колеса 1 і 2 з'єднуються зворотною пасовою передачею по зовнішньому ободу колеса 1 (радіус ) і внутрішньому ободу колеса 2 (радіус ).

Швидкість точок паса і швидкість точок коліс по зазначених радіусах однакова і дорівнює:

. Звідси маємо .

При зворотній (перехресної) пасовій передачі напрямок обертання коліс 1 і 2 протилежний. Тому кутова швидкість спрямована за рухом годинникової стрілки.

Колеса 2 і 3 зв'язані між собою зубчастим зачепленням по зовнішніх радіусах коліс. Тому спільна для обох коліс точка контакту має швидкість:

. Звідси маємо .

При зовнішнім зачепленні напрямок обертання коліс протилежний, тобто колесо 3 обертається проти руху годинникової стрілки.

Вантаж 5 зв'язаний з колесом 3 за допомогою нерозтяжної нитки, намотаної на внутрішній обід колеса. У цьому випадку спільною точкою зв’язку рухів тіл 5 і 3 є точка дотику колеса й нитки, яка має таку ж швидкість як вантаж, тобто:

. У момент часу 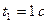маємо .

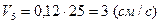Напрямок руху вантажу визначається напрямком обертання колеса 3, тобто вантаж має швидкість , спрямовану вниз.

2. Визначимо швидкість точки 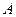колеса 3 в момент часу .

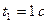Точка 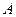належить колесу 3, яке обертається з кутовою швидкістю і розташована на відстані від осі його обертання. Тому її швидкість:

. При 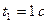одержимо .

Вектор спрямований по дотичній до обода вбік обертання колеса 3 (рис.К2.б).

3. Визначимо прискорення тіл.

Знаючи закон руху рейки, визначимо її прискорення:

і при .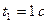

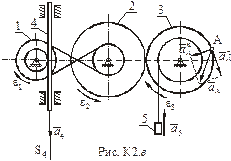Маємо > 0, тому вектор спрямований у напрямку осі , тобто вниз (рис.К2.в).

Кутове прискорення колеса 1 залежить від дотичного прискорення точки з'єднання з рейкою, що збігається з прискоренням .

Таким чином маємо:

. При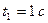

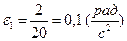
Якщо вектор спрямований вниз, то напрямок - за рухом годинникової стрілки.

Точки з'єднання коліс 1 і 2 мають однакові дотичні прискорення. Тому справедливо: .

Тоді при .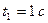

Кутове прискорення спрямоване протилежно пришвидшенню , тобто проти руху годинникової стрілки.

За аналогією можна записати , тобто при 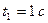маємо

. Напрямок прискорення 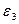протилежний, тобто за рухом годинникової стрілки.

Прискорення вантажу 5:

Вектор спрямований вгору.

4. Визначення прискорення точки .

Точка належить колесу 3, яке обертається з кутовою швидкістю і з кутовим прискоренням 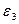. Відстань точки від осі обертання - .

Модуль прискорення точки визначимо за формулою:

Дотичне прискорення точки :

Вектор 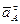прикладений у точці і спрямований по дотичній до обода колеса 3 у напрямку кутового прискорення .

Нормальне прискорення точки :

Вектор прикладений у точці і спрямований до осі обертання колеса 3.

Таким чином: .

Напрямок повного прискорення точки визначається векторною сумою векторів 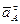і (рис.К2.в).

	Кінематичні характеристики тіл 1-5 і точки : 1. Колесо 1 - ; 2. Колесо 2 - ; 3. Колесо 3 - ; 4. Рейка 4 - ; 5. Вантаж 5 - ; 6. Точка - Напрямок векторів швидкостей і прискорень – рис.К2,б,в.

Відповідь.

3. Динаміка

Дата добавления: 2015-10-31