Після|потім| зрівнювання

У попередньому підрозділі знайдено| співвідношення (10.28), яке дозволяє оцінювати значення середньої квадратичної похибки| m виміряних|виміряти| величин до зрівнювання. Виникає справедливе питання. Чи зміниться ця величина після|потім| зрівнювання?

Щоб|аби| відповісти на це питання приведемо доведення теореми відоме з|із| теорії похибок.

Теорема 10.1. Середнє значення відношення квадрата середньої квадратичної похибки після зрівнювання до квадрата середньої квадратичної похибки до зрівнювання, тобто її середнє зменшення, обумовлене зрівнюванням системи виміряних величин способом найменших квадратів, дорівнює відношенню числа необхідних вимірів до всіх вимірів, тобто:

де – середня квадратична похибка виміряних величин після зрівнювання, t – число необхідних вимірів, n – число всіх вимірів.

Доказ

Для зручності і простоти доведення теореми запроваджуватимемо обмеження на кількість невідомих. Вважатимемо|гадатимемо|, що система лінеаризованих рівнянь поправок (10.7) містить|утримує| три невідомих і n рівнянь. Тоді в матричному вигляді систему рівнянь поправок можна записати наступним чином|виді|:

, (10.32)

де, – зрівняні значення вільних членів.

Представимо|уявлятимемо| співвідношення|ставлення| (2.31) у виді:

де = .

Значення – функції поправок . Знайдемо формульні співвідношення доданків , , формули (10.33). Для цього продиференціюємо початкові рівняння поправок (10.7) по змінних і враховуючи результати доведення основної теореми похибок і раніше отримані формули (10.19) і (10.20) представимо середні квадратичні похибки у вигляді добутку Якобіанів:

Розділимо праву і ліву частину отриманого рівняння на і проведемо необхідні операції з Якобіанами. Крім того, враховуючи рівноточність вимірів отримаємо:

(a)

Аналогічно, для , отримаємо:

(b)

(c)

(d)

Підставляючи (а), (b), (c) і (d) у формулу (10.33) підсумуємо добутки , , виносячи за дужки вагові коефіцієнти . В результаті знайдемо шукане значення:

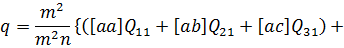
(10.35)

.

Із властивостей операцій над матрицями в лінійній алгебрі відомо, що

,

де Е – одинична матриця, у якої діагональні елементи дорівнюють 1, а недіагональні – 0. У формулі (10.35) суми добутків в круглих дужках, враховуючи (10.13) і (10.21) є добутками i-го рядка матриці А на i-й стовпець матриці 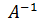. Отже, вони відповідають діагональним елементам матриці Е, які дорівнюють 1. Тоді на підставі (10.31), (10.33) і (10.35) можна записати:

При трьох невідомих і поширюючи отриману рівність на будь-яке число невідомих, остаточно отримаємо:

що і потрібно було довести (див. формулу 10.31).

Таким чином, зрівнювання методом найменших квадратів підвищує в середньому точність результатів вимірів.

10.7. Зрівнювання і оцінка точності при нерівноточних| вимірах|вимірах|

У попередньому підрозділі розглядалася оцінка точності тільки рівноточних вимірів. Відомо, що у разі нерівноточних вимірів точність виміряних величин характеризується вагами . Отже, і вільні члени в рівняннях поправок:

,

що є функціями виміряних величин, також матимуть ваги .

Зрівнювання результатів вимірів проводитимемо з урахуванням умов: Розглянемо деяку функцію . Згідно тверджень, зроблених в п.п. 6.2 вагу цієї функції можна прирівняти до 1

Отже, оскільки у цьому випадку нерівноточні вимірювання можна звести до рівноточних. Для цього достатньо кожне рівняння системи поправок помножити на , тобто систему лінійних рівнянь поправок можна записати у загальному вигляді:

.

Запишемо цю систему рівнянь в матричному вигляді|виді|:

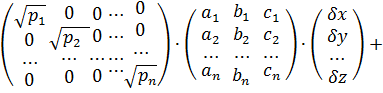
З метою звільнення від знаку радикала, а також перетворення формули (10.37) до виду нормальних рівнянь помножимо її праву і ліву частини на добуток . Отримаємо:

,(10.38)

де

.

Спростимо формулу (10.38). Для цього позначимо матрицю коефіцієнтів нормальних рівнянь:

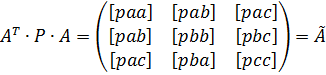. (10.39)

Вектор-стовпець | вільних членів нормальних рівнянь позначимо:

. (10.40)

Для дотримання умов побудови нормальних рівнянь вектор-стовпець прирівняємо до нуля. Отримаємо:

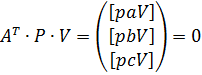. (10.41)

З введеними|запроваджувати| позначеннями система нормальних рівнянь набуде вигляду:

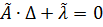. (10.42)

Отримане матричне рівняння як і у разі рівноточних вимірів, вирішується шляхом множення його зліва на зворотну матрицю:

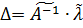. (10.43)

При нерівноточних вимірах аналогічно вирішується і завдання оцінки точності невідомих з використанням формули:

.

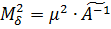Емпірична середня квадратична похибка |одиниці ваги обчислюється за формулою:

Таким чином, видно|показний|, що зрівнювання нерівноточних| вимірів|вимірів| принципово не відрізняється від зрівнювання рівноточних вимірів|вимірів||.

Дата добавления: 2015-10-29