Приклад|зразок| 10.1.

Якщо шуканими невідомими є координати x, y пунктів геодезичної мережі, то сукупна похибка положення пункту в даній системі координат відповідно до виразу (10.21) характеризується матрицею:

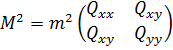. (10.23)

Отримана|одержувати| формула дає можливість|спроможність| розрахувати наступні точності| характеристики положення|становища| точки|точки| на площині|площині|:

1. Середні квадратичні похибки по осях координат і 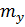, обчислювані за формулами (10.22). Вони залежать від вибору системи координат (рис. 10.1).

2. Кругову середню квадратичну похибку|, обчислювану за формулою:

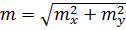, (10.24)

яка знайшла широке застосування|вживання| в геодезичній практиці, при цьому виходячи з припущення|гадки|, що розсіювання вимірів по осях X і Y має однакову ймовірність.

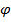
b

P

a

U

X

Y

V

Рис. 10.1 – Ілюстрація для прикладу|приміром| 10.1

3. Еліпс похибок, орієнтація і розміри осей якого визначають найбільш вірогідні напрями|направлення| і величину максимальної і мінімальної середньої квадратичної похибки| положення геодезичного пункту.

Для визначення сукупної похибки положення геодезичного пункту скористаємося співвідношенням (10.23) і рис. 10.1, де показано, що поворотом осей навколо точки Р можна підібрати таку систему координат UV, при якій недіагональні елементи матриці Q дорівнюватимуть нулю і даний вираз матиме вигляд:

. (10.25)

Необхідний для такого перетворення кут|ріг| повороту осей обчислюється за формулою:

а елементи 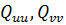на основі рівнянь:

.

Велика і мала піввісь еліпса похибок будуть відповідно дорівнювати:

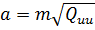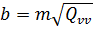, . (10.27)

Таким чином, детально розглянута|розглядувати| процедура (див. п.п.10.3 процедура 12) оцінювання точності зрівняних|урівнювати| значень невідомих. На прикладі|зразку| демонструється послідовність обчислення точнісних|підрахунку| |характеристик.

10.5. Обчислення|підрахунок| емпіричної середньої квадратичної похибки|

Дата добавления: 2015-10-29