За поправками, одержаними|одержувати| із|із| зрівнювання.

Як правило, виміряні величини визначені за умови:

,

тобто є підстава припускати, що на їх основі можна отримати спроможну і незміщену оцінку середньої квадратичної похибки m. Проте, на підставі цієї ж умови і здорового глузду можна стверджувати, що сума квадратів дійсних похибок завжди буде більша суми квадратів отриманих поправок. Тоді справедлива нерівність де Δ – дійсні похибки. Розділивши цю нерівність на n, отримаємо:

Отже, величина буде спроможною, але зміщеною оцінкою m. Для того, щоб вона виявилася незміщеною, необхідно знаменник правої частини зменшити на деяку, поки невідому, величину u.

Тоді справедливо записати емпіричну середню квадратичну похибку в наступному вигляді:

В даному випадку, задача зводиться до визначення невідомої величини u.

Проаналізуємо вираз (10.28) і перш за все, відзначимо, що загальне число вимірів n не може бути менше числа необхідних вимірів, тобто 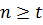. Звідси витікає, що u не може бути більше t, оскільки при знаменник у формулі (10.28) дорівнюватиме нулю. Отже .

Зробимо припущення, що . При завдання зрівнювання не виникає, поправки 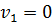, ,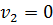…, , отже і , що суперечить здоровому глузду, оскільки .

Це дає підставу,|основу| формулу (10.28) записати у виді:

Наведений доказ рівності (10.29) заснований на припущеннях і евристичних міркуваннях тому не є|з'являється| суворим|суворим|. Існує і строгий|суворий| доказ, який є громіздким і в теперішньому курсі не розглядається|розглядує|.

З тієї причини, що емпірична середня квадратична похибка| m найчастіше визначається із невеликої кількості вимірів, її надійність визначає середня квадратична похибка, яка обчислюється за формулою:

Таким чином, на основі умов мінімізації суми квадратів поправок розглянутий|розглядувати| наближений спосіб оцінювання їх точності за результатами зрівнювання.

Середня квадратична похибка виміряних|виміряти| величин

Дата добавления: 2015-10-29