Історична довідка

Лагранж Жозеф Луї (25.1.1736, Турин, — 10.4.1813, Париж), французький математик та механік, член Паризької АН (1772). Самостійно вивчав математику. В 19 років став професором в артилерійській школі Турина. В 1759 обраний членом Берлінської Академії наук, а в 1766 – 1787 р. був її президентом. З 1795 р. професор нормальної школи. Лагранжу належать також видатні дослідження з різноманітних питань математичного аналізу (формула залишкового члена ряду Тейлора, формула кінцевих приростів, теорія умовних екстремумів), теорії чисел, алгебри (симетричної функції коренів рівняння), з диференціальних рівнянь (теорія особливих рішень, метод варіації сталих), з інтерполяції, математичної картографії, астрономії та ін.    

Характеристика П’єром Симоном Лапласом діяльності Лагранжа …серед тих, хто найефективнішим чином розширив границі наших знань, Ньютон та Лагранж в найвищому ступені володіли щасливим мистецтвом відкриття нових даних, які являють собою сутність знань… Характеристика Франсуа Марі Шарлем Фур’є діяльності Лагранжа Усім своїм життям… він довів свою відданість загальним інтересам людства, — шляхетною простотою манер, величним характером і, нарешті, точністю та глибиною своїх наукових праць.      

Використаємо доведення теореми Лагранжа. Для цього розглянемо функцію

, (11.7)

де – невизначені множники – корелати, які пов’язують між собою умовні змінні .

Перетворимо функцію Ф в систему рівнянь, прирівнявши послідовно кожну складову формули (11.7) до нуля

,

а потім прирівняємо до нуля систему з рівнянь з невідомими. В скороченому вигляді можна записати:

.

Для складання функції Лагранжа помножимо (11.6) на невизначені множники . Отримані вирази підсумуємо і додамо до функції .

В результаті математичних перетворень отримаємо функцію

.

Знайдемо локальні мінімуми в цій функції. Для цього візьмемо часткові похідні за змінними і прирівняємо їх до нуля,

Із отриманої системи рівнянь знаходимо поправки , ,

,

,

Представимо отриману систему рівнянь в матричному вигляді:

або в скороченому вигляді

(11.8)

Із отриманого співвідношення видно, що для обчислення поправок до виміряних величин необхідно спочатку визначити матрицю К, яка являє собою вектор невизначених множників Лагранжа, тобто корелат …,

.

Підставимо матрицю із співвідношення (11.8) до формули (11.6) і отримаємо:

(11.9)

Введемо позначення

. (11.10)

На підставі співвідношення (11.9) і введеного позначення (11.10) можна записати:

. (11.11)

Отриманий вираз являє собою систему нормальних рівнянь, де кількість рівнянь r дорівнює кількості невідомих , .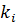

Помножимо (11.10) слева на обратную матрицу 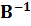, находим столбец коррелат

. (11.12)

Підставимо значення матриці К у вираз (11.8), знайдемо стовпчик поправок V.

Контроль правильності перетворень здійснюють наступною процедурою. Помножимо вираз (11.8) зліва на транспоновану матрицю-рядок поправок . Отримаємо

.

Виконавши необхідні перетворення, знайдемо , але так як , то 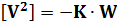, що і підтверджує правильність перетворень.

Упорядкуємо розглянуті вище математичні перетворення і задамо строгий порядок процедур зрівнювання виміряних величин, пов’язаних умовами.

Процедура 1. Визначення кількості і виду умовних рівнянь в системі виміряних геодезичних величин.

Процедура 2. Складання умовних рівнянь з нев’язками , та їх обчислення.

Процедура 3. Приведення отриманих рівнянь до лінійного вигляду шляхом розкладення їх у ряд Тейлора (11.4 -11.6).

Процедура 4. Складання матриці коефіцієнтів нормальних рівнянь корелат (11.10).

Процедура 5. Обчислення корелат 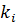, з рівняння (11.11).

Процедура 6. Визначення вірогідніших поправок підставленням корелат в рівняння (11.8).

Процедура 7. Контроль правильності виконаних математичних перетворень.

Таким чином, розглянута процедура знаходження умовного мінімуму методом найменших квадратів. Приведена послідовність розв’язання нормальних рівнянь корелат.

Дата добавления: 2015-10-29