Постановка задачі. Умовні рівняння

Вище (див. п.9.2) було відзначено, що існують два підходи до рішення задач зрівнювання систем виміряних геодезичних величин. Один з них параметричний спосіб, який викладено в п.10. Тепер розглянемо другий спосіб – зрівнювання виміряних величин, пов’язаних умовами (корелатний спосіб).

Ідея корелатного способу полягає в знаходженні поправок до виміряних величин через допоміжні невизначені множники, які називають корелатами. Сутність зрівнювання коре латним способом полягає в тому, що задачу знаходження мінімуму функції рівняння розкладеного в ряд Тейлора вирішують способом Лагранжа з визначенням корелат, у результаті чого отримують корелатні рівняння поправок (вектори поправок). Перетворивши рівняння поправок, отримують нормальні рівняння корелат, через які знаходять вірогідніші значення поправок.

Деталізуємо сказане і будемо вважати, що рівно точно виміряні n величин 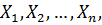пов’язаних незалежними математичними умовами

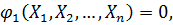
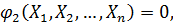
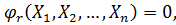(11.1)

де 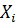, – істинні значення виміряних величин.

Загальна кількість таких умов дорівнює кількості надлишкових вимірів. Внаслідок неминучих похибок результати рівноточних вимірів 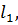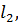…, 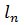не будуть точно задовольняти умовам (11.1). У результаті в правій частині системи рівнянь (11.1) справедливо записати деяку величину, яка відрізняється від нуля. Такі величини прийнято називати нев’язками, тобто

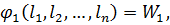
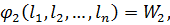
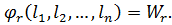(11.2)

Сутність задачі полягає в тому, щоб знайти такі поправки 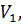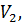…, 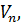до виміряних величин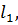 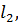…, , 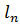які забезпечували б виконання умов (11.1), тобто

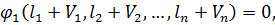
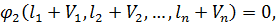
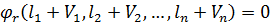(11.3)

Так як кількість невідомих в отриманій системі умовних рівнянь більша за кількість рівнянь, 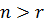, то вона не має однозначного розв’язання і є невизначеною.

Для того щоб знайти поправки 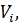, які найкращим чином зрівнювали б виміряні величин, скористаємося вже відомим методом найменших квадратів .

Для цього необхідно привести умовні рівняння до лінійного вигляду, розклавши при цьому рівняння (11.3) в ряд Тейлора і обмежуючись при цьому першими членами ступеневого ряду, що мають степінь одиницю, отримаємо:

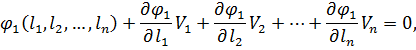
Введемо позначення, як це було зроблено в п.10.1 при постановці задачі зрівнювання поправок параметричним способом.

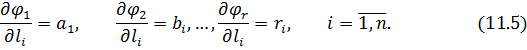
З урахуванням введених позначень (11.5), а також нев’язок, які є складовими перших частин системи рівнянь (11.2) представимо умовні рівняння в лінійному вигляді:

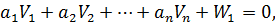
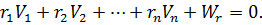
Або в матричному вигляді:

Таким чином, сформульована задача зрівнювання виміряних величин, пов’язаних умовами методом найменших квадратів, а також показаний шлях перетворення рівнянь до лінійного вигляду і представлення їх в матричному вигляді.

Дата добавления: 2015-10-29