В) Скалярний добуток в координатах

Нехай е₁, е₂,..., е_п – довільний базис евклідового простору V, х =х₁ е₁ +х₂ е₂ +...+х_п е_п, у =у₁ е₁ +у₂ е₂ +...+у_п е_п – два довільні вектори цього простору. Тоді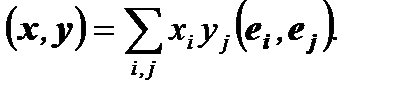

Якщо базис е₁, е₂, ..., е_п – ортонормований, то

( x, y )=x₁y₁+x₂y₂+…+x_ny_n.

Помноживши обидві частини рівності х =х₁ е₁ +х₂ е₂ +...+х_п е_п скалярно на е_і, отримаємо, що (х, е_і )=х_і, тобто і -та координата вектора х в ортонормованому базисі дорівнює скалярному добутку вектора х на одиничний вектор е_і. Цей скалярний добуток називають проекцією вектора х на вектор е_і. Отже, координати вектора в ортонормованому базисі – це його проекції на базисні вектори.

Г) Ортогональне доповнення

Два підпростори V₁ та V₂ евклідового простору V називаються взаємно ортогональними, якщо кожний вектор із V₁ ортогональний кожному вектору із V₂ (позначають V₁ 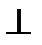V₂).

Теорема 3. Для того, щоб підпростори V₁ та V₂ були взаємно ортогональними, необхідно і достатньо, щоб всі базисні вектори одного були ортогональні всім базисним векторам другого.

Теорема 4. Два взаємно ортогональних підпростори перетинаються по нульовому вектору.

Теорема 5. Кожний вектор х із V, ортогональний V₁, належить V₂.

Підпростір V₂, утворений всеможливими векторами із V, ортогональними до всіх векторів із V₁, називається ортогональним доповненням V₁. Позначають його .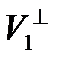

Підпростори V₁ і V₂ породжують V і перетинаються по нульовомувектору. Значить, евклідів простір V являє собою пряму суму довільного свого підпростору і його ортогонального доповнення:

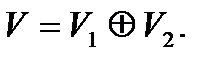
Тому кожний вектор х із V можна однозначно подати у вигляді суми

x = y + z, де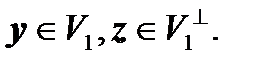

Лінійні перетворення в евклідовому просторі

А) Перетворення, спряжене до даного

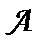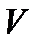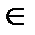Нехай – лінійне перетворення евклідового простору . Лінійне перетворення , для якого при всіх x, y V

(A x, y) = (x, A^* y), називається спряженим до A.

Властивості:

1. .

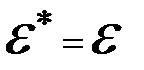Дійсно, (x, 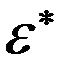y) = ( 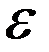x, y) =(x, y) = (x, 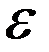y).

2. .

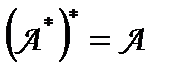Дійсно, (A x, y) = (x, A* y) = (A* y, x) = (y,(A*)^* x) = ((A*)^* x, y).

3. .

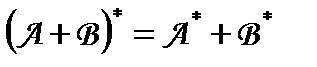Дійсно, (x,(A + B) * y) = ((A + B) x, y) = (A x + B x, y) = (A x, y) + (B x, y) =

= (x, A* y) + (x, B* y) = (x,(A^* + B*) y).

4.

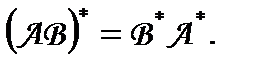
Дійсно, (x,(AB) * y) = ((AB) x, y) = (A (B x), y) = (B x, A* y) = (x, B^* (A*) y) = (x,(B ^*A*) y).

5. Якщо 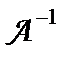існує, то .

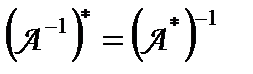Дійсно, .

Дата добавления: 2015-10-29