Изменение координат тензора при замене базиса

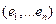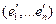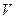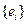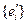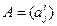Пусть и - два базиса в пространстве . Обозначим через матрицу перехода от базиса к базису . Элементы матрицы индексируем так: , где 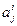- элемент i-ой строки и j-ого столбца. Тогда имеем:

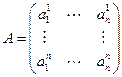и .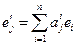

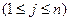Это стандартное обозначение: чтобы суммирование велось по индексу, встречающемуся сверху и снизу. В некоторых книгах знак суммы опускают и пишут: 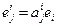. Но мы так делать не будем: все суммы будем прописывать полностью.

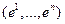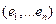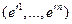Пусть теперь - дуальный базис к базису , а - дуальный к базису 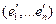в пространстве . Обозначим через 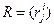матрицу перехода от базиса 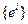к базису 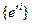в пространстве . Тогда 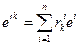. Чтобы следовать правилу “разных уровней” (т.е. чтобы индекс суммирования появился сверху и снизу), обозначим через 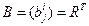- транспонированная матрица 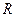. Тогда 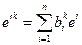. Эту формулу мы запишем следующим образом. Поскольку 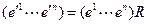, то 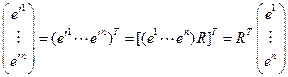, т.е. 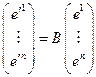. Введём вспомогательную матрицу 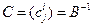. Тогда 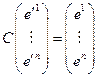, т.е. 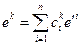. Т.к. базисы дуальны 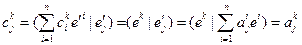. Т.е. 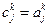и 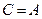. Отсюда .

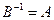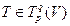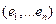Пусть теперь и - его координаты в , а 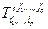- координаты в базисе 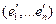. Тогда

, .

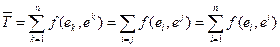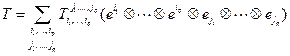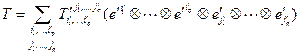(6)

Выразим 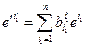(аналогично выражаем 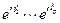) и подставим в формулу (6). Получим

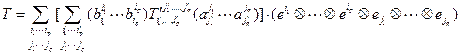. Здесь мы использовали, что 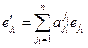и аналогичные выражения для 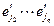. Т.к. элементы 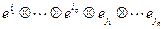образуют базис пространства 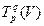, то нами доказана следующая

Теорема. При переходе от базиса 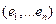к базису 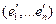в 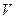координаты тензор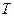а типа 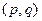изменяются по правилу: 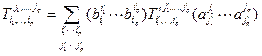, где 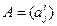- матрица перехода от базиса 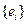к базису 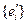пространств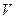а , а .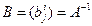

6. Свёртки тензоров.

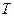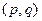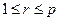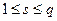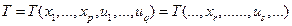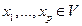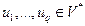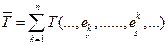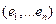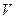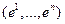Пусть - тензор типа . Зафиксируем числа и , и определим свёртку по r-ому ковариантному индексу и s-ому контрвариантному индексу следующим образом. Т.к. , где , а , то можно определить сумму , где - базис , а - дуальный базис .

Определение. 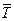называется свёрткой тензора 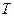по r-ому ковариантному индексу и s-ому контрвариантному индексу.

Ясно, что 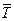- полилинейная функция от оставшихся аргументов, т.е. 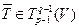. Докажем, что 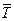не зависит от выбора базиса пространства .

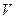Доказательство: пусть 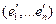- другой базис пространств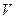а , а 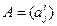- матрица перехода от базиса 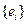к базису 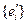. Тогда 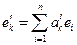. Напомним, что для дуальных базисов имеем: 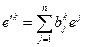, где 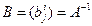(смотри доказательство предыдущей теоремы). Зафиксируем для удобства все остальные переменные у 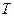кроме и 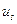, обозначим 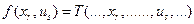. Тогда 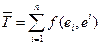. Получаем: .

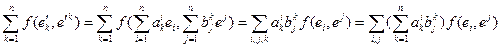Заметим, что 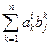- произведение i-ой строки матрицы на j-ый столбей матрицы . Т.к. 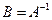эта сумма равна , .

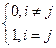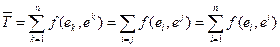23.04.2005

Связь координат тензора T и его свертки .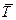

Теорема. Свертка по s-тому ковариантному и r-тому контравариантному индексам тензора T типа (p,q) является тензором типа (p-1,q-1) с координатами

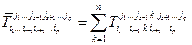
То, что свертка – тензор типа 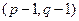- проверено. Пусть 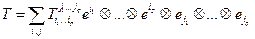, где 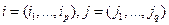. Как и раньше, обозначим через 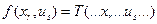. Обозначим 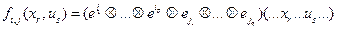. Тогда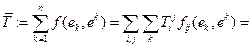

.

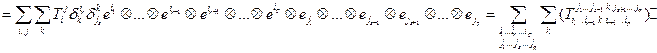
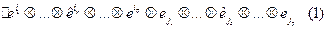Знак «домик» означает пропуск соотв. индекса (т.е. 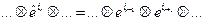). Соотношение (1) и есть утверждение теоремы.

Пример. Тензор типа (1,1) 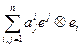- это матрица 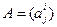. Его свертка равна 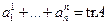- след матрицы A.

Дата добавления: 2015-10-26