Квадрики в аффинном пространстве

Квадратичные функции в аффинном пространстве

Отображение 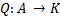называют квадратичной функцией, если 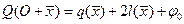, (1)

где 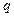- квадратичная форма на 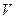, a .

Задача Показать, что если 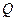задана формулой (1) с фиксированной точкой , для любой другой точки выполняется соотношение .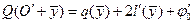

Опр. Ранг квадратичной функции : .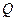

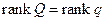Координатная запись

Пусть 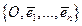- система координат в и , .

Тогда (2)

Центральная точка

Пусть , , . Пусть также - полярная к 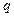билинейная симметрическая форма на 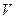. Тогда

,

т.е. .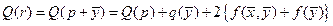

Опр. Точку называют центром (или центральной точкой) 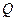, если

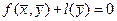
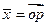Другими словами (3), где (т.е. ).

В координатной записи центральной точки это означает, что если начало координат является центральной точкой квадрики, то линейная часть 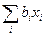в формуле (2) отсутствует.

Опр. - множество всех центральных точек .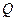

Нахождение центра

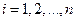Пусть , . Тогда , (4)

Т.е. (4) – критерий центральной точки .

Теорема. Множество центральных точек квадратичной функции 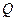, заданной формулой (2) в системе координат 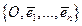, состоит из точек , где - решение системы

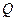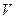уравнений (4). Если - одна из центральных точек , то , где - гиперплоскость в . В частности - аффинное подпространство в .

Уже, показано, что задаётся С.Л.У.(4). Если она совместна, то множество её решений – аффинная плоскость в с направляющим пространством , заданным системой , . Но это система уравнений , т.е. .

Приведение квадратичной функции к каноническому виду.

Теорема. Пусть 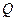- квадратичная функция ранга на 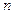-мерном аффинном пространстве над K. Если 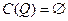, то и в некоторой системе координат 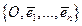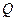приводится к виду

, (5) где .

Если 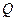имеет непустой , то существует система координат 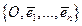с началом в центральной точке , в которой 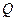приводится к виду:

(6)

При этом и значение 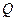в любой центральной точке равно .

Выберем в 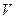канонический базис 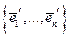для 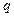. Для произвольной точки 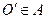в системе координат функция 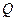имеет вид (для ): 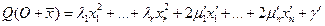, причём , т.к. .

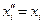
Замена координат вида , ; , т.е. перенос начала координат в соответствующую точку к виду

.

Если все 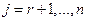, то 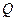имеет вид (6)

Пусть . Возьмём и положим

, , ,..., , ,…, .

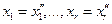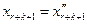Тогда в новых координатах 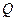будет иметь вид (5).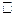

11.04.05

ТЕНЗОРЫ

Основные понятия.

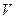Пусть - произвольное поле, - векторное пространство над , 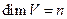. Обозначим через дуальное пространство, т.е. пространство линейных функций . 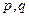- неотрицательные целые числа. Для каждой такой пары определим следующее понятие:

Определение: Тензором н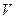а типа 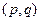называют любое полилинейное отображение

.

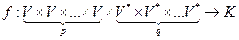Т.е. 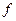- функция от аргументов, первые из которых из пространства 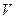, следующие - из пространства , линейная по каждому из аргументов со значениями в поле .

Определение: Число называют валентностью (реже ранго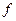м) . Сам 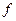называют смешанным тензором раз ковариантным, раз контрвариантным.

Дата добавления: 2015-10-26