
Читайте также:
|
Опр.  - квадратичная форма, если $ симметричная билинейная форма
- квадратичная форма, если $ симметричная билинейная форма  , такая, что
, такая, что 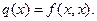 В этом случае говорят, что
В этом случае говорят, что 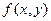 - полярная билинейная форма для q.
- полярная билинейная форма для q.
Предложение. Полярная БФ определена однозначно, если 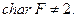
 ð
ð
Опр. Матрица квадратичной формы q в базисе 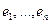 - матрица ее полярной БФ.
- матрица ее полярной БФ. 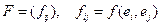
Пример. Пусть  для
для  . Тогда
. Тогда 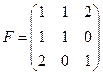 .
.
Опр. Ранг квадратичной формы – ранг полярной БФ.
Опр. 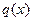 - невырожденная квадратичная форма, если
- невырожденная квадратичная форма, если 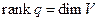 (т.е.
(т.е. 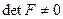 )
)
Опр. Канонический вид квадратичной формы 
Опр. Нормальный вид квадратичной формы  , и все
, и все 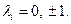
Алгоритм Лагранжа (приведения к каноническому виду).
Пусть 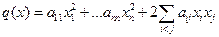 . Метод заключается в выделении полных квадратов.
. Метод заключается в выделении полных квадратов.
ð (1) Пусть 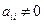 , например,
, например,  . Тогда
. Тогда 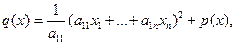 где
где 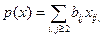 т.е. p (x) не зависит от x 1. Положим
т.е. p (x) не зависит от x 1. Положим 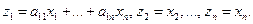
Тогда 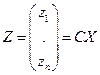 , где
, где  Следовательно,
Следовательно, 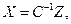 и можно считать, что C -1 - матрица перехода к некоторому новому базису, в котором вектор
и можно считать, что C -1 - матрица перехода к некоторому новому базису, в котором вектор 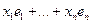 имеет вид
имеет вид 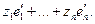
По индукции $ невырожденная замена переменных  такая, что
такая, что  Положим
Положим  Тогда
Тогда 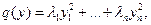 где
где 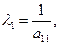 и
и  - координаты в некотором базисе, т.к. Y = DX, и
- координаты в некотором базисе, т.к. Y = DX, и 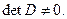
(2) Предположим, что  Пусть
Пусть 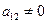 . Сделаем замену
. Сделаем замену 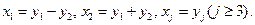 Тогда
Тогда  и
и 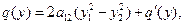 где в
где в 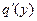 нет
нет 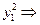 Далее как в п. (1).
Далее как в п. (1).
(3) Все 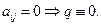 ð
ð
8. Вещественные квадратичные формы
Пусть V – пространство над 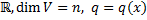 - квадратичная форма на V. Тогда в V существует базис, в котором q (x) имеет нормальный вид
- квадратичная форма на V. Тогда в V существует базис, в котором q (x) имеет нормальный вид 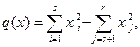 где
где 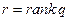 - не зависит от выбора базиса.
- не зависит от выбора базиса.
Теорема. (закон инерции) Число положительных и отрицательных коэффициентов в нормальном виде квадратичной формы не зависит от выбора базиса (т.е. s и r-s всегда одни и те же).
Пусть 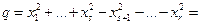 (в базисе
(в базисе 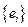 )
) 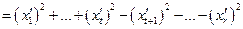 (в базисе
(в базисе 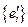 ). Предположим, что t < s. Обозначим
). Предположим, что t < s. Обозначим 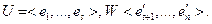 Тогда
Тогда 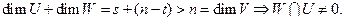 Пусть
Пусть 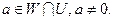 Т.к.
Т.к. 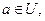 то
то 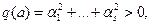 где
где 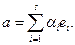 Аналогично, q (a) £ 0 т.к.
Аналогично, q (a) £ 0 т.к. 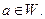 Противоречие. Следовательно, t не может быть меньше s и наоборот. ð
Противоречие. Следовательно, t не может быть меньше s и наоборот. ð
Опр. Если 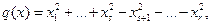 то s – положительный индекс инерции, а число (r – s) – отрицательный индекс инерции q.
то s – положительный индекс инерции, а число (r – s) – отрицательный индекс инерции q.
Опр. Квадратичные формы p (x) и q (x) эквивалентны, если существует невырожденная матрица A, такая, что 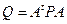 , где P и Q – матрицы p и q.
, где P и Q – матрицы p и q.
Следствие. Формы p(x) и q(x) эквивалентны Û  положительные и отрицательные индексы инерции совпадают.
положительные и отрицательные индексы инерции совпадают.
ð 1) Ü Приведем к нормальному виду.
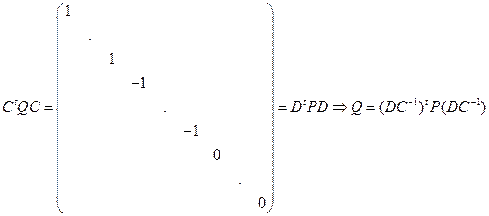
2) Þ аналогично. ð
Дата добавления: 2015-10-26; просмотров: 110 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Единственность ЖНФ | | | Ортогональные дополнения |