Доказательство. 1) Мы уже доказали, что

1) Мы уже доказали, что

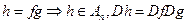
Это и означает, что гомоморфизм групп ,

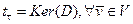
Гомоморфизм сюръективен.

Пусть теперь 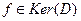. Тогда .

Докажем, что этим свойством обладает только сдвиг.

Заметим, сначала, что если 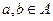, , то , .

Поэтому .

Вектор не зависит от , так как если , то .

Обозначим . Тогда , то есть . В ядре, кроме сдвигов, ничего нет.

2) Очевидно, что -подгруппа в A_n. Так как

не содержит сдвигов, то ограничение D на H инъективный гомоморфизм . Покажем теперь его сюръективность. Построим нужное аффинное преобразование. Пусть , где F произвольный невырожденный оператор на V.

Тогда если , то , то есть f -аффинное преобразование, причем и .

Следовательно, -изоморфизм групп.

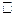
Теорема. Любое аффинное преобразование можно представить в виде композиции 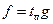, где .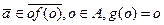

Возьмем , положим 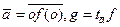. Тогда g -аффинно-линейное преобразование. . Очевидно, .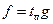

Координатная запись аффинных преобразований

Пусть система координат в аффинном пространстве и –аффинное преобразование с линейной частью .

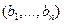Пусть F – матрица в базисе , а – координаты точки в той же системе координат, то есть . p - точка с координатами .

Тогда . Если - координаты вектора 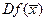, то .

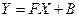То есть . Отсюда и если – координаты ,то или , где .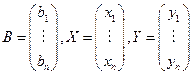

4 апреля 2005

n=3 Примеры движений

Собственное

Векторное движение – поворот вокруг некоторой прямой и сдвиг на вектор, параллельный оси вращения, т.е.

Частные случаи – сдвиг или вращение

Несобственное

1) вращение с отражением

2) скользящая симметрия (отражение относительно некоторой плоскости и сдвиг на вектор, параллельный )

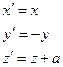
Теорема. Любое собственное движение трёхмерного евклидового пространства является винтовым движением. Любое несобственное движение является либо вращением с отражением, либо скользящей симметрией.

Пусть - евклидово пространство, , 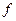- движение. В 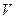существует ортонормированный базис , , 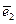, канонический для . Зафиксируем начало координат – точку . Тогда

1) или 2) 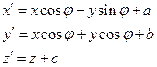или 3) 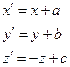или 4)

Случай 1

,

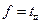Случай 2

Как и при n=2 находим такие, что

Тогда после переноса начала координат в точку имеем

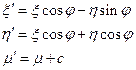
в новых координатах. Т.е. 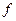- винтовое движение.

Случай 3

Вводим новые координаты: , , 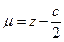. Тогда

т.е. это сдвиг на вектор и отражение относительно плоскости .

Случай 4

Ищем точку , , 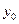как решение системы

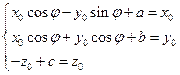
Это возможно, т.к. матрица невырождена .

Переносим начало координат в точку , получаем

В новых координатах это поворот в плоскости с отражением относительно этой плоскости.

Дата добавления: 2015-10-26