
|
Читайте также: |
I случай. Пусть А<0, В>0, С=0.
Докажем, что  с
с  [a, b]: f(с)=0.
[a, b]: f(с)=0.
Положим a1=a, b1=b.
f(a1)=А<0, f(b1)=В>0.
Разделим отрезок [a1, b1] пополам. Тогда возможны два случая:
либо f( )=0 и с=
)=0 и с=  , f(с)=0;
, f(с)=0;
либо f( )
)  0 (f(
0 (f(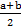 )
)  0).
0).
Если f( )>0, то рассмотрим [a2, b2]= [a1,
)>0, то рассмотрим [a2, b2]= [a1,  ], если f(
], если f( )<0, то рассмотрим отрезок [a2, b2]= [
)<0, то рассмотрим отрезок [a2, b2]= [  , a1]
, a1]  f(a2)<0, f(b2)>0.
f(a2)<0, f(b2)>0.
Разделим отрезок [a2, b2] пополам. Тогда либо f( )=0 и теорема доказана; либо f(
)=0 и теорема доказана; либо f( )
)  0 и мы возьмём так же, как и на первом шаге отрезок [a3, b3]
0 и мы возьмём так же, как и на первом шаге отрезок [a3, b3] 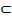 [a2, b2]
[a2, b2] 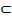 [a1, b1], дл.[a3, b3]=
[a1, b1], дл.[a3, b3]=  (b2–a2)=
(b2–a2)=  дл.[a2, b2], f(a3)<0, f(b3)>0.
дл.[a2, b2], f(a3)<0, f(b3)>0.
Продолжим этот процесс. Тогда либо на конечном шаге мы найдём нужную точку с  [a1, b1]= [a, b]: f(с)=0, либо мы построим последовательность вложенных отрезков [an, bn] таких, что
[a1, b1]= [a, b]: f(с)=0, либо мы построим последовательность вложенных отрезков [an, bn] таких, что  n: дл.[an, bn]=
n: дл.[an, bn]=  дл.[a1, b1]=
дл.[a1, b1]=  и f(an)<0, f(bn)>0.
и f(an)<0, f(bn)>0.
Тогда по теореме о вложенных отрезках
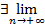 an=
an= 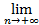 bn=с
bn=с 
 n: с
n: с  [an, bn]
[an, bn]  с
с  [a1, b1]= [a, b].
[a1, b1]= [a, b].
 f(x) непрерывна на промежутке X, [a, b]
f(x) непрерывна на промежутке X, [a, b] 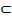 X, то f(x) непрерывна на [a, b], а, следовательно, и в точке с
X, то f(x) непрерывна на [a, b], а, следовательно, и в точке с 
 f(an)=
f(an)=  f(bn)= f(с).
f(bn)= f(с).
Но согласно теореме о предельном переходе в неравенствах для одной последовательности f(an)<0  f(с)
f(с)  0 и f(bn)>0
0 и f(bn)>0  f(с)
f(с)  0
0  f(с)=0.
f(с)=0.
II случай. Пусть А<В.
Докажем, что  С: А<С<В
С: А<С<В  с
с  [a, b]: f(с)=С.
[a, b]: f(с)=С.
Рассмотрим функцию f1(x)= f(x) –С. Она непрерывна на X по теореме об арифметических свойствах непрерывных функций.
А–С= f(a) –С= f1(a)<0, f1(b)=В –С= f(b) –С>0.
Тогда выполняются условия I-го случая 
 с
с  [a, b]: f1(с)=0
[a, b]: f1(с)=0  f1(с)= f(с) –С=0
f1(с)= f(с) –С=0  f(с)=С.
f(с)=С.
III случай. Пусть А>В.
Тогда  С: В<С<А
С: В<С<А  с
с  [a, b]: f(с)=С.
[a, b]: f(с)=С.
Рассмотрим функцию f2(x)= – f(x).
Из условия –В> –С> –А следует f2(a)= – f(a)= –А< –С< –В= f2(b)= – f(b).
f2(x) непрерывна на X, следовательно, и на [a, b]. Для неё выполняются условия случая II.
f2(a)= –А, f2(b)= –В 
 с
с  [a, b]: f2(с)= –С=–f(с)
[a, b]: f2(с)= –С=–f(с)  f(с)=С.
f(с)=С.
Замечание 1.
Теорема 1, в частности, верна и когда X=[a, b] и f(x) непрерывна на [a, b].
Замечание 2.
Для функции, заданной на стандартной области определения X, состоящей из нескольких промежутков, и непрерывной на X, теорема 1 применима к каждому промежутку отдельно.
Замечание 3.
Содержание теоремы 1 кратко состоит в том, что если X – промежуток и f(x) непрерывна на нём, то область значения f(x) Y={y; y= f(x), х  Х} так же промежуток (то есть непрерывная функция отображает промежуток на промежуток).
Х} так же промежуток (то есть непрерывная функция отображает промежуток на промежуток).
Теорема 2. (Первая теорема Вейерштрасса об ограниченности функции непрерывной на отрезке.)
Любая функция, непрерывная на отрезке, ограничена на нём.
Дата добавления: 2015-10-30; просмотров: 131 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Классификация точек разрыва функции. | | | Доказательство. |