
|
Читайте также: |
Доказательство теоремы 2.
Рассмотрим функцию f1(х)· f2(х) на Х и возьмём произвольную последовательность {хn} типа Гейне ( n: хn
n: хn  Х,
Х,  n: хn
n: хn  хо,
хо,  хn= хо) и соответствующую последовательность значений функций f1(хn)· f2(хn).
хn= хо) и соответствующую последовательность значений функций f1(хn)· f2(хn).
А так как по условию теоремы 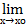 f1(х)= L1
f1(х)= L1 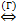
 {хn}, а значит и для нашей {хn} (
{хn}, а значит и для нашей {хn} ( n: хn
n: хn  Х,
Х,  n: хn
n: хn  хо,
хо,  хn= хо):
хn= хо):  f1(хn)= L1,
f1(хn)= L1,
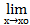 f2(х)= L2
f2(х)= L2 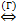
 {хn}, а значит и для нашей {хn}:
{хn}, а значит и для нашей {хn}:  f2(хn)= L2.
f2(хn)= L2.
А тогда по теореме о произведении двух сходящихся последовательностей:
 f1(хn)· f2(хn)=
f1(хn)· f2(хn)= 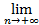 f1(хn)·
f1(хn)· 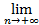 f2(хn)= L1·L2
f2(хn)= L1·L2  так как {хn} была вфбрана произвольно, то
так как {хn} была вфбрана произвольно, то 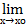 f1(х)· f2(х)= L1·L2.
f1(х)· f2(х)= L1·L2.
Теорема 4.
Пусть f(х) имеет стандартную область определения Х, хо лежит внутри или является концом одного из промежутков, образующих Х, и пусть f(х) в точке хо имеет предел L. Тогда он единственен.
Доказательство.
Пусть L=(Г) 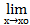 f(х). Утверждение теоремы непосредственно следует из определения предела функции в точке в смысле Гейне и единственности предела сходящейся последовательности.
f(х). Утверждение теоремы непосредственно следует из определения предела функции в точке в смысле Гейне и единственности предела сходящейся последовательности.
Теорема 5.
Пусть f(х) имеет стандартную область определения Х, хо лежит внутри или является концом одного из промежутков, образующих Х. f(х) в точке хо имеет предел L  когда f(х) представима в виде
когда f(х) представима в виде  х
х  Х: f(х)=L+
Х: f(х)=L+  (х), где
(х), где 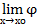 (х)=0.
(х)=0.
Доказательство.
1. Необходимость.
Пусть 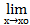 f(х)= L. Обозначим f(х)- L =
f(х)= L. Обозначим f(х)- L =  (х)
(х) 
 х
х  Х: f(х)= L+
Х: f(х)= L+  (х).
(х).
Докажем, что 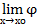 (х)=0.
(х)=0.
Действительно, 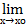 f(х)=(К) L
f(х)=(К) L 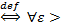 0
0 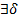 >0
>0  х (
х ( х
х  Х, х
Х, х  хо,
хо,  │x - хо│<
│x - хо│<  ): │
): │  (х)│=│f(х)- L│<
(х)│=│f(х)- L│< 
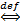
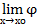 (х)=0.
(х)=0.
2. Достаточность.
Дано: 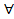 х
х  Х: f(х)= L+
Х: f(х)= L+  (х), где
(х), где 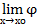 (х)=0.
(х)=0.
Докажем, что 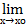 f(х)= L.
f(х)= L.
По условию,  х
х  Х: f(х)= L+
Х: f(х)= L+  (х), то
(х), то  (х)= f(х)- L
(х)= f(х)- L
и т.к. 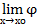 (х)=0
(х)=0 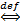
 0
0 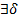 >0
>0  х (
х ( х
х  Х, х
Х, х  хо,
хо,  │x - хо│<
│x - хо│<  ): │
): │  (х)│= │f(х)- L│<
(х)│= │f(х)- L│< 
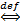
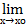 f(х)= L.
f(х)= L.
Теорема 6. (об устойчивости знака функции, имеющей в точке предел)
Пусть f(х) имеет стандартную область определения Х, хо лежит внутри или является концом одного из промежутков, образующих Х, и пусть f(х) имеет предел в точке хо равный L  0.
0.
Тогда  -окрестность точки хо такая, что на множестве {(хо-
-окрестность точки хо такая, что на множестве {(хо-  , хо)}
, хо)}  {(хо, хо+
{(хо, хо+  )}
)}  Х функция f(х) имеет тот же знак, что и L.
Х функция f(х) имеет тот же знак, что и L.
Доказательство.
Пусть 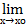 f(х)= L, L
f(х)= L, L  0. Возьмём
0. Возьмём  =
= 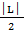 >0.
>0.
Тогда  0, а значит и для
0, а значит и для  =
= 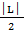 >0,
>0, 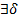 >0
>0  х (
х ( х
х  Х, х
Х, х  хо,
хо,  │x - хо│<
│x - хо│<  ):│ f(х)- L│<
):│ f(х)- L│<  =
= 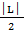
 L
L  <f(х)< L+
<f(х)< L+ 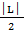
1) Пусть L>0  │L│=L.
│L│=L.
Тогда х  {(хо-
{(хо-  , хо)}
, хо)}  {(хо, хо+
{(хо, хо+  )}
)}  Х: 0<L-
Х: 0<L-  =
=  <f(х)< L+
<f(х)< L+ 
 0<
0<  <f(х)
<f(х)  f(х)>0.
f(х)>0.
2) Пусть L<0.  │L│= - L.
│L│= - L.
 х
х  {(хо-
{(хо-  , хо)}
, хо)}  {(хо, хо+
{(хо, хо+  )}
)}  Х: L+
Х: L+  <f(х)<L-
<f(х)<L- 

 L<
L< 
 f(х)<0
f(х)<0
Определение.
Функция f(х) называется ограниченной на множестве Х, если f(х) ограничена на Х и снизу, и сверху.
Теорема 7. (о локальной ограниченности функции, имеющей в точке предел).
Пусть f(х) имеет стандартную область определения Х, точка хо лежит внутри или является концом одного из промежутков, образующих Х, и пусть f(х) имеет в точке хо предел, равный L. Тогда на множестве (хо  хо+
хо+  )
)  Х f(х) ограничена.
Х f(х) ограничена.
Дата добавления: 2015-10-30; просмотров: 149 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство. | | | Доказательство. |