
Читайте также:
|
Введение.
Математический анализ – это классическая часть современной геометрии. Развитие именно современной геометрии началось с публикации Н.И.Лобачевского¹ работы «О началах геометрии» 1829, в которой была решена проблема V постулата Евклида о параллельных. Н.И.Лобачевский доказал, что V постулат Евклида не вытекает из остальных постулатов и поэтому возможна другая геометрия. Он назвал её воображаемой, а мы сейчас называем её неевклидовой или геометрией Лобачевского. Первое сообщение было сделано 23.02.1826 г. В Казанском Университете.
Открытие Лобачевского:
(1) Лишило всякого смысла мысль о врождённости геометрических (понятий) объектов;
(2) Заставило глубже вникнуть в смысл геометрических понятий;
(3) Чрезвычайно важным оказалось осознание того факта, что логическая структура геометрии не определяет природы геометрических объектов.
Это означает, что в качестве „точек”, „прямых”, „плоскостей” в разных случаях можно подразумевать разные предметы (объекты).
Каждый конкретный выбор этих объектов даёт конкретную „модель” геометрии.
§2. Множества.
С конца 19 века наиболее универсальным языком математики стал язык теории множеств. Основателем теорий множеств является немецкий математик Георг Кантор². Кантор говорил: „… под множеством мы понимаем объединение в одно целое определённых объектов, вполне различных, нашей интуиции или нашей мысли”. На рубеже 19-го и 20-го веков на Конгрессе математиков в 1900 году отмечалось, какую огромную пользу принёс теоретико-множественный язык для развития математики.
А в 1902 году Б. Рассел³ обнаружил парадокс, оказавшийся классическим парадоксом, схожим с парадоксом Зенона (например, о брадобрее). Оказалось, что высказывание – “множество всех множеств” – противоречиво.
Если в теории, где-то противоречие, то как же пользоваться её результатами? Опасно! Значит, наивное представление о множестве не так уже просто и безобидно. Высказывание Кантора трудно принять за определение. Поэтому логики подвергают понятие множества тщательному анализу, в который мы углубляться не будем.
Заметим, что в существующих аксиоматических теориях множество определяется как математический объект, обладающий определённым набором свойств. Описание этих свойств составляет аксиоматику. Любая из существующих аксиоматик такова, что она с одной стороны избавляет от известных противоречий наивной теории множеств, а с другой стороны – обеспечивает свободу оперирования с конкретными множествами, возникающими в различных отделах математики и в первуюочередь в математическом анализе (в широком смысле слова – как современной геометрии).
X – множество; x  X – x элемент множества X.
X – x элемент множества X.
Определение.
Множество, не содержащее элементов, называется пустыммножеством и обозначается  .
.
Определение.
Множество А называется конечным, если оно состоит из конечного числа элементов.
Определение.
Пусть даны два множества А и В. А  , В
, В  и пусть каждый элемент x
и пусть каждый элемент x  А является элементом множества В, т.е. x
А является элементом множества В, т.е. x  В. Тогда А называется подмножеством множества В, обозначается А
В. Тогда А называется подмножеством множества В, обозначается А 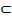 В.
В.
Замечание.
Для любого множества А, А≠  , следует А
, следует А 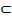 А (из определения).
А (из определения).
Определение.
Пусть X – произвольное множество. X и  называются несобственными подмножествами множества X.
называются несобственными подмножествами множества X.
Определение.
Пусть X – непустое множество и А 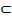 X, А
X, А  и пусть существует x
и пусть существует x  X такой, что x
X такой, что x 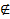 А. Тогда А называется собственным подмножеством множества X.
А. Тогда А называется собственным подмножеством множества X.
Простейшие операции над множествами.
Пусть X – произвольное непустое множество и А 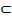 X.
X.
Определение.
| A B |
| X |
Разностью между множествами А и В называется множество, обозначаемое А  В либо пустое, либо состоящее из тех элементов множества А, которые непринадлежат множеству В.
В либо пустое, либо состоящее из тех элементов множества А, которые непринадлежат множеству В.
Определение.
Пусть А 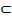 X. Дополнением множества А в X называется X
X. Дополнением множества А в X называется X  А. оно обозначается СхА=СА= X
А. оно обозначается СхА=СА= X  А.
А.
Пусть задана совокупность множества Аα, где {α}=y – совокупность индексов.
Определение.
Объединением 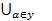 Аα множеств Аα, α
Аα множеств Аα, α  y называется множество, каждый элемент которого (если он существует) принадлежит хотя бы одному Аα, т.е. либо
y называется множество, каждый элемент которого (если он существует) принадлежит хотя бы одному Аα, т.е. либо 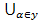 Аα =
Аα =  , либо условие x
, либо условие x 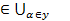 Аα равносильно условию – существует α
Аα равносильно условию – существует α  y такое, что x
y такое, что x  Аα.
Аα.
Определение.
Пересечением множеств Аα, α  y, называется множество, каждый элемент которого (если он существует) принадлежит каждому множеству Аα, α
y, называется множество, каждый элемент которого (если он существует) принадлежит каждому множеству Аα, α  y. Обозначается пересечение множеств Аα, α
y. Обозначается пересечение множеств Аα, α  y через
y через  .
.
Задача.
Доказать, что если X – непустое множество и для всех α  y Аα
y Аα  X, то
X, то
(1) X  )=
)=  (1) Сх
(1) Сх 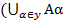 )=
)= 
(2) X  (
( )=
)=  (2) Сх(
(2) Сх( )=
)= 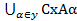
§3. Понятие множества действительных чисел.
Определение (аксиоматическое).
Непустое множество  ={x} элементов x произвольнойприроды называется множеством действительных чисел, если выполняются следующие условия:
={x} элементов x произвольнойприроды называется множеством действительных чисел, если выполняются следующие условия:
I На множестве  введена операция сложения элементов, т.е. указан закон, согласно которому каждой упорядоченнойпаре элементов x, y из
введена операция сложения элементов, т.е. указан закон, согласно которому каждой упорядоченнойпаре элементов x, y из  поставлен в соответствие элемент из
поставлен в соответствие элемент из  обозначаемый x+y и называемый суммой элементов x и y так, что выполняются следующие (аксиомы сложения) условия:
обозначаемый x+y и называемый суммой элементов x и y так, что выполняются следующие (аксиомы сложения) условия:
(1)I В  существует единственный нейтральный элемент (называемый нулём при сложении)
существует единственный нейтральный элемент (называемый нулём при сложении)  такой, что для любого x
такой, что для любого x  выполнено:
выполнено:
x+  =
=  +x=x
+x=x
(2)I Для каждого x  существует единственный элемент из
существует единственный элемент из  , называемый противоположным элементу x, обозначаемый (-x) и такой, что
, называемый противоположным элементу x, обозначаемый (-x) и такой, что
x+(-x)=(-x)+x= 
(3)I Для любых x, y, z 
x+(y+z)=(x+y)+z (ассоциативность)
(4)I Для любых x, y из 
x+y=y+x (коммутативность)
II На множестве  введена операция умножения элементов, т.е. указан закон, согласовано которому каждойупорядоченнойпаре элементов x, y из
введена операция умножения элементов, т.е. указан закон, согласовано которому каждойупорядоченнойпаре элементов x, y из  поставлен в соответствие элемент из
поставлен в соответствие элемент из  называемый произведением x на y и обозначаемый xy так, что выполнены следующие условия (аксиомы умножения):
называемый произведением x на y и обозначаемый xy так, что выполнены следующие условия (аксиомы умножения):
(1)II В  существует единственный нейтральный элемент (единица при умножении) обозначаемый 1 такой, что для любого x
существует единственный нейтральный элемент (единица при умножении) обозначаемый 1 такой, что для любого x  :
:
x·1=1·x=x
(2)II Для любого x  {
{  } существует единственный элемент из
} существует единственный элемент из  , называемый обратным к x и обозначаемый x-1 такой, что:
, называемый обратным к x и обозначаемый x-1 такой, что:
x· x-1= x-1·x=1
(3)II Для любых x, y, z из  :
:
x·(y·z)=(x·y)·z (ассоциативность)
(4)II Для любых x, y, z из  :
:
x·y=y·x (коммутативность)
(I, II) – Связь между сложением и умножением.
В  для любых x, y, z:
для любых x, y, z:
(x+y)·z=x·z+y·z (дистрибутивность)
III На  задано отношениепорядка
задано отношениепорядка  , т.е. для любых двух элементов x, y
, т.е. для любых двух элементов x, y  установлено: выполняется или нет x
установлено: выполняется или нет x  (x меньше или равно
(x меньше или равно  ).
).
При этом отношение  удовлетворяет следующим аксиомам порядка:
удовлетворяет следующим аксиомам порядка:
(1)III Для любого x из  :
:
x  (рефлексивность)
(рефлексивность)
(2)III Если для двух x и y: x  y и y
y и y  x, то x=y (x есть y)
x, то x=y (x есть y)
(3)III Если для x, y, z  выполнено:
выполнено:
x  y и y
y и y  z, то x
z, то x  z (транзитивность)
z (транзитивность)
(4)III Для любых x, y, z  , если x
, если x  y, то
y, то
x+z  y+z
y+z
(5)III Для любых x, y из  , либо x
, либо x  y, либо y
y, либо y  x (либо и то и другое)
x (либо и то и другое)
(6)III Для x, y  , если 0
, если 0  x, 0
x, 0  y, то 0
y, то 0  xy
xy
Замечание.
1. По определению x  означает, что y
означает, что y  x.
x.
2. Как следствие получаем, что для любых x, y  имеет место одно и только одно из соотношений:
имеет место одно и только одно из соотношений:
x  y, x=y, x
y, x=y, x  y.
y.
IV Аксиома Архимеда.
Для любого элемента с  , удовлетворяющего условию 0
, удовлетворяющего условию 0  с; существует натуральное число n>с.
с; существует натуральное число n>с.
V Аксиома полноты (непрерывности).
Для любых двух непустых множеств X={x} и Y={y}, X  , Y
, Y  , удовлетворяющих условию: для любых x
, удовлетворяющих условию: для любых x  , y
, y  x
x  y, существует элемент с
y, существует элемент с  такой, что для любого x
такой, что для любого x  и любого y
и любого y  : x
: x  , с
, с  y, т.е. x
y, т.е. x 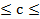 y.
y.
Определение.
Каждый элемент множества  называется действительным числом.
называется действительным числом.
Приведённая система аксиом непротиворечива, т.к. существуют множества, удовлетворяющие I – V.
Например.
Десятичная форма числа, двоичная форма числа.
Замечание.
Единственность нейтральных элементов по сложению и умножению, а также противоположного и обратного элемента может быть выведена из аксиом и их единственность можно не требовать заранее.
Определение.
Непустое множество G, удовлетворяющее I: (1)I - (3)I называется аддитивной или абелевой 4 группой.
Определение.
Непустое множество  , удовлетворяющее условиям I(1-4), II(1-4), (I, II) называется полем.
, удовлетворяющее условиям I(1-4), II(1-4), (I, II) называется полем.
Определение.
Непустое множество  , удовлетворяющее условиям называется линейно упорядоченным полем.
, удовлетворяющее условиям называется линейно упорядоченным полем.
Определение.
Непустое множество, удовлетворяющее условиям I, II, III, IV называется архимедовым полем.
Определение.
Действительные числа 1, 1+1=2, 2+1=3, … называются натуральными числами.
Множество 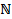 всех натуральных чисел содержит 1 и вместе с каждым n
всех натуральных чисел содержит 1 и вместе с каждым n 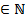 содержит n+1.
содержит n+1.
Определение.
Все натуральные числа, все им противоположные и нуль образуют множество всех целых чисел.
Определение.
Число вида p·q-1= p·  где q
где q 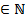 , p
, p  называется рациональным числом.
называется рациональным числом.
Множество всех рациональных чисел обозначается  .
.
Определение.
Каждое действительное число, не являющееся рациональным, называется иррациональным.
§4. Отображения множеств.
Определение.
Пусть X и Y два непустых множества. Говорят, что задано отображение f множества X „в” множество Y, если указан закон, согласно которому элементу x  поставлен в соответствие элемент y
поставлен в соответствие элемент y  .
.
Обозначение f: X  Y; X
Y; X  Y.
Y.
Если y=f(x), x  , y
, y  , то y называется образом x при отображении f, а x при этом называется прообразом y при отображении f.
, то y называется образом x при отображении f, а x при этом называется прообразом y при отображении f.
Множество Yf = {y; y=f(x), x  }
} 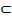 Y называется образом множества X при отображении f.
Y называется образом множества X при отображении f.
Определение.
Говорят, что два непустых множества X и Y равны, если каждый элемент x  принадлежит Y (X
принадлежит Y (X 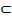 Y) и каждый элемент y
Y) и каждый элемент y  принадлежит X (Y
принадлежит X (Y 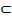 X), то есть
X), то есть
X=Y  X
X 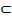 Y и Y
Y и Y 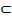 X.
X.
Определение.
Говорят, что задано отображение f множества X „на” множество Y, если Yf =Y.
Определение.
Отображение f: X  Y называется взаимно-однозначным, если разным x из X ставятся в соответствие разные y из Y.
Y называется взаимно-однозначным, если разным x из X ставятся в соответствие разные y из Y.
Определение.
Говорят, что два непустых множества X и Y являются равномощными, если между ними можно установить взаимно-однозначное отображение.
Определение.
Множество, равномощное множеству 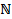 натуральных чисел называется счётным.
натуральных чисел называется счётным.
Определение.
Бесконечное множество, не являющееся счетным, называется несчётным.
Утверждение 1. (Доказать самостоятельно).
Любое бесконечное множество содержит счётное подмножество.
Утверждение 2. (Доказать самостоятельно).
Любое бесконечное подмножество счётного множества счётно.
Теорема 1.
Множество  всех рациональных чисел счётно.
всех рациональных чисел счётно.
Доказательство.
Рассмотрим множество  всех рациональных чисел и расположим их следующим образом:
всех рациональных чисел и расположим их следующим образом:
0 1 -1 2 -2 3 -3 …
 -
- 
 -
- 
 -
- 
 …
…
 -
- 
 -
- 
 -
- 

… … …
Отметим место каждого числа.
Теорема 2. (Кантора). (Без доказательства).
Множество  действительных чисел несчётно.
действительных чисел несчётно.
Задача.
Где больше чисел?
§  Точные грани (верхняя и нижняя) числовых множеств.
Точные грани (верхняя и нижняя) числовых множеств.
Примеры.
X= 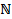 ={1, 2, …, n, n+1, …}
={1, 2, …, n, n+1, …}
X ={x; 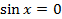 }
}
X= (-  , +
, +  )
)
X={r; r – рационально: r2<2}
Определение.
Числовое множество X называется ограниченным сверху (снизу), если существует такое число В (соответственно А), что для любого x  : x
: x  В (соответственно А
В (соответственно А  x).
x).
Определение.
Числовое множество X называется ограниченным, если оно ограниченно и сверху и снизу.
Определение.
Пусть X – ограниченное сверху числовое множество. Точной верхней гранью множества X называется наименьшее из всех чисел, ограничивающих множество X сверху, и оно обозначается supX= sup{x}.
Определение.
Пусть X – ограниченное снизу числовое множество. Точной нижней гранью множества X называется наибольшее из всех чисел, ограничивающих множество X снизу. Оно обозначается infX=inf{x}.
Дадим рабочую форму этих понятий.
Определение.
Пусть X – ограниченное сверху числовое множество. Число M= supX называется точной верхней гранью множества X, если:
(1) для любого x  : x
: x  M.
M.
(2) для каждого  >0 существует
>0 существует 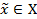 такой, что M-
такой, что M-  <
<  .
.
Определение.
Пусть X – ограниченное снизу числовое множество. Число m= infX называется точной нижней гранью множества X, если:
(1) для любого x  : m
: m  x.
x.
(2) для каждого  >0 существует
>0 существует  такой, что
такой, что  <m+
<m+  .
.
Иногда случается, что числовое множество X имеет наибольший (наименьший) элемент, т.е. существует  (соответственно
(соответственно  ) такой, что для любого x
) такой, что для любого x  : x
: x  (соответственно x
(соответственно x  .
.
Утверждение.
Пусть  - наибольший элемент множества X. Тогда
- наибольший элемент множества X. Тогда  .
.
Дата добавления: 2015-10-30; просмотров: 156 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Автономная некоммерческая организация | | | Доказательство. |