
|
Читайте также: |
1. Необходимость.
Пусть а= 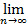 xn. Рассмотрим последовательность {
xn. Рассмотрим последовательность {  n}={ xn-а}.
n}={ xn-а}.
а  xn для каждого
xn для каждого  >0 существует номер N такой, что для любого номера n>N: │xn-а│<
>0 существует номер N такой, что для любого номера n>N: │xn-а│< 
 │
│  n│<
n│< 
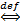 0=
0= 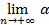 n.
n.
2. Достаточность.
Пусть дана последовательность { xn} и для каждого n, n=1, 2, …: xn=а+  n, где {
n, где {  n} – б.м.
n} – б.м.
Докажем, что а= 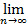 xn.
xn.
{  n} – б.м.
n} – б.м.  для каждого
для каждого  >0 существует номер N такой, что для каждого номера n>N: │
>0 существует номер N такой, что для каждого номера n>N: │  n│<
n│< 
 │
│  n│=│xn-а│<
n│=│xn-а│< 
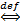 а=
а=  xn.
xn.
Свойства бесконечно малых последовательностей.
I Лемма 1.
Пусть {  n} б.м. Тогда для любого числа А
n} б.м. Тогда для любого числа А  : {
: { 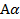 n} – б.м.
n} – б.м.
Доказательство.
1. А=0. Тогда для любого n, n=1, 2, …: А  n=0
n=0  n=0
n=0 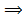 {
{ 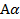 n} – б.м.
n} – б.м.
2. {  n} - б.м.
n} - б.м. 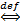 для каждого
для каждого  >0, а значит для
>0, а значит для  >0 существует номер N такой, что для любого номера n>N:
>0 существует номер N такой, что для любого номера n>N:
│  n│<
n│< 
 │А│∙│
│А│∙│  n│=│А
n│=│А  n│<
n│< 
 0=
0= 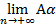 n
n  {
{ 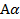 n} б.м.
n} б.м.
II Лемма 2.
Сумма двух бесконечно малых последовательностей бесконечно мала.
Доказательство.
Пусть заданы две б.м. последовательности {  n} и {
n} и {  n}. Рассмотрим последовательность {
n}. Рассмотрим последовательность {  n+
n+  n } и докажем, что она б.м.
n } и докажем, что она б.м.
{  n} – б.м.
n} – б.м. 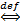 для каждого
для каждого  >0, а значит и для
>0, а значит и для  >0 существует номер N1 такой, что для любого номера n>N1: │
>0 существует номер N1 такой, что для любого номера n>N1: │  n│<
n│< 
{  n} – б.м.
n} – б.м. 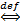 для каждого
для каждого  >0, а значит и для
>0, а значит и для  >0 существует номер N2 такой, что для любого номера n>N2: │
>0 существует номер N2 такой, что для любого номера n>N2: │  n │<
n │<  .
.
Тогда  n>N=max{N1, N2}: │
n>N=max{N1, N2}: │  n+
n+  n│
n│  │
│  n │+│
n │+│  n │<
n │< 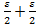 =
= 

 n+
n+  n)=0
n)=0
III Лемма 3.
Произведение б.м. последовательности на ограниченную последовательность – б.м.
Доказательство.
Пусть {  n} – б.м., {
n} – б.м., {  n} ограничена. Докажем, что {
n} ограничена. Докажем, что { 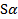 n} – б.м.
n} – б.м.
Так как {  n} ограничена
n} ограничена  существует M>0 такое, что для любого n, n=1, 2, …: │
существует M>0 такое, что для любого n, n=1, 2, …: │  n│
n│  M.
M.
Если положить А= -M, а В=M, то для любого n: А  n
n  В
В
 n=0
n=0  для каждого
для каждого  >0,
>0,  >0 существует номер N такой, что для любого номера n>N: │
>0 существует номер N такой, что для любого номера n>N: │  n│<
n│<  .
.
Тогда для любого номера n>N: │  n∙
n∙  n│=│
n│=│  n│∙│
n│∙│  n│<
n│<  ∙M=
∙M=  .
.
§3. Свойства сходящихся последовательностей.
Теорема 1.
Любая сходящаяся последовательность имеет единственный предел.
Доказательство. (от противного)
Пусть существует {xn}, такая сходящаяся последовательность, для которой существуют два числа а и b, а<b, такие что
а=  xn, b=
xn, b=  xn, b>a.
xn, b>a.
так как a<b, то существуют непересекающиеся окрестности точек а и b.
| a |

|
| X |
Возьмём  =
=  (b-а)>0.
(b-а)>0.
а=  xn
xn 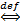 для каждого
для каждого  >0, а значит и для
>0, а значит и для  =
=  (b-а)>0 существует номер N1 такой, что для любого n> N1: │ xn-а│<
(b-а)>0 существует номер N1 такой, что для любого n> N1: │ xn-а│<  (b-а).
(b-а).
b=  xn
xn 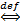 для каждого
для каждого  >0, а значит и для
>0, а значит и для  =
=  (b-а)>0 существует номер N2 такой, что для любого номера n>N2: │xn-b│<
(b-а)>0 существует номер N2 такой, что для любого номера n>N2: │xn-b│<  (b-а).
(b-а).
Тогда для любого n>N=max{N1, N2} выполняются оба неравенства:
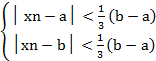

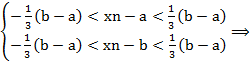


 b-
b-  xn<a+
xn<a+ 
 b-
b-  a+
a+ 
 b-a<2
b-a<2  =
= 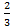 (b-а), что невозможно.
(b-а), что невозможно.
Мы пришли к противоречию.
Теорема 2.
Любая сходящаяся последовательность ограничена. Обратное неверно.
Дата добавления: 2015-10-30; просмотров: 139 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство. | | | Доказательство. |