
Читайте также:
|






При определении отрицания предложениями и операций над предложениями важнейшим является согласование об истинности исходного предложения.
Таблица истинности.
| А | В | Ā | А V В | А Л В | А  В В
|
| ист | ист | л | ист | ист | ист |
| ист | л | л | ист | л | л |
| л | ист | ист | ист | л | ист |
| л | л | ист | л | л | ист |
Недоумение может вызвать „ист” в нижнем правом углу таблицы. Дело в том, что предложение А  В равносильно предложению
В равносильно предложению 
 А
А 

 В.
В.
Тогда если А – ложно, то  - истинно и дизъюнкция
- истинно и дизъюнкция  В истинно.
В истинно.
Таким образом, импликация беззащитна против ввода неверных данных.
§2. Предикаты.
Рассмотрим следующие высказывания.
1) … больше 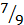 .
.
2) ∘∘∘∘  ‒ ‒ ‒ ‒
‒ ‒ ‒ ‒
3) *** есть отец ~~~~
4) ∙∙∙∙∙∙∙ + ‒‒‒‒‒<*****
Это предикаты, своего рода заготовки для предложений.
Определение.
Предикатом называется высказывание, содержащее одно или несколько пустых мест и обращающиеся в предложение всякий раз, когда пустые места (переменные) замещены конкретными предметами, принадлежащими некоторым определённым классам объектов.
Пустые места будем обозначать буквами x, y, z, …, а сами предикаты буквами P, Q, R, ….
P(x) – предикат, содержащий одно переменное.
Q(x, y) – предикат, содержащий две переменные (два пустых места).
Примеры предикатов.
1. x> 
2. x 
3. z отец υ
4. x+y<ω
Над предикатами можно производить такие же действия, как и над предложениями.
В то же время в отличи от предложений предикаты не могут быть ни истинными, ни ложными.
§3. Кванторы.
Замещение пустых мест в предикате не единственный способ получения предложений.
Пусть P(x)  x – певец мужского хора МИФИ.
x – певец мужского хора МИФИ.
Условимся замещать x – всеми мальчиками, присутствующими в аудитории на лекции.
Символ  условимся читать как „каждый” или „любой”, или „все”, а символ
условимся читать как „каждый” или „любой”, или „все”, а символ  - как „существует”, „найдётся” или „есть хоть один”.
- как „существует”, „найдётся” или „есть хоть один”.
Тогда  P(x) – все присутствующие поют в хоре МИФИ.
P(x) – все присутствующие поют в хоре МИФИ.
 x: P(x) – среди присутствующих есть хоть один, поющий в хоре МИФИ.
x: P(x) – среди присутствующих есть хоть один, поющий в хоре МИФИ.
Определение.
Символы  называются квантором общности и квантором существования соответственно.
называются квантором общности и квантором существования соответственно.
Q(x, y)  x прочитал y.
x прочитал y.
{y} – произведения де Сент-Экзюпери.
x – присутствующие в аудитории.
 x
x  : Q(x, y) (v)
: Q(x, y) (v)

 : Q(x, y) (vv)
: Q(x, y) (vv)
В математике в тех случаях, когда А  В истинно, то говорят, что В является необходимым условием для А, а А – достаточным условием для В.
В истинно, то говорят, что В является необходимым условием для А, а А – достаточным условием для В.
При построении отрицания предложения, полученного воздействием кванторов на предикат все объекты остаются на своих местах, каждый квантор общности  яется на квантор существования
яется на квантор существования  , а каждый квантор существования
, а каждый квантор существования  заменяется на квантор общности
заменяется на квантор общности  и над предикатом ставится черта.
и над предикатом ставится черта.
Примеры.
1. (А)  ({xn} ограничена)
({xn} ограничена)  ({xn} ограничена сверху)
({xn} ограничена сверху)  ({xn} ограничена снизу)
({xn} ограничена снизу)  (
( В
В  n: xn
n: xn  В)
В)  (
( А
А  n: А
n: А  xn)
xn)
( )
)  ({xn} неограниченна)
({xn} неограниченна)  ({xn} неограниченна сверху)
({xn} неограниченна сверху)  ({xn} неограниченно снизу)
({xn} неограниченно снизу)  (
( В
В  n: xn>В)
n: xn>В)  (
(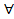 А
А  n: А>xn)
n: А>xn)
2. (В)  ({xn} монотонна)
({xn} монотонна)  ({xn} убывает)
({xn} убывает)  ({xn} возрастает)
({xn} возрастает)  (
( : xn
: xn  xn+1)
xn+1)  (
( : xn
: xn  xn+1)
xn+1)
( )
)  ({xn} не является монотонной)
({xn} не является монотонной)  ({xn} неубывающая)
({xn} неубывающая)  ({xn} невозрастающая)
({xn} невозрастающая)  (
( : xń<xń+1)
: xń<xń+1)  (
( ň: xň>xň+1)
ň: xň>xň+1)
3. (С)  ({xn} сходится)
({xn} сходится)  (
( а: а=
а: а= 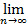 xn)
xn)  (
( а
а  >0
>0  N
N  n>N: │xn - а│<
n>N: │xn - а│<  )
)
( )
)  ({xn} расходится)
({xn} расходится)  (
( а
а  >0
>0  N
N  n: │xn - а│
n: │xn - а│  )++++++++
)++++++++
4. (D)  ({xn} б.м.)
({xn} б.м.)  (0=
(0= 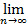 xn)
xn)  (
( >0
>0  N
N  : │xn│<
: │xn│<  )
)
( )
)  ({xn} не является б.м.)
({xn} не является б.м.)  (
( >0
>0  N
N  : │xn│
: │xn│  )
)
§4. Предельный переход в неравенствах. (Глава 2)
Теорема 1. (Для одной последовательности).
Пусть {xn} сходится и 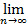 xn=а, и пусть
xn=а, и пусть  В такое, что
В такое, что  n, n=1, 2, …: xn
n, n=1, 2, …: xn  В (
В ( А
А  : xn
: xn  А).
А).
Тогда а  В (соответственно, А
В (соответственно, А  а).
а).
Дата добавления: 2015-10-30; просмотров: 155 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство. | | | Доказательство. |