
|
Читайте также: |
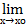 f(х)= L
f(х)= L 
 0, а значит и для
0, а значит и для  =1>0
=1>0 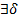 >0
>0  х (
х ( х
х  Х, х
Х, х  хо,
хо,  │x - хо│<
│x - хо│<  ): │f(х)- L│<
): │f(х)- L│<  =1
=1  L-1<f(х)<L+1
L-1<f(х)<L+1
а) Пусть хо  Х.
Х.
Положим A=min{L-1, f(хo)},
B=max{L+1, f(хo)}.
Тогда  х
х  (хо
(хо  хо+
хо+  )
)  Х: А
Х: А  f(х)
f(х)  В.
В.
б) хо 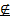 Х.
Х.
Положим  Тогда
Тогда  х
х  (хо
(хо  хо+
хо+  )
)  Х: А
Х: А  f(х)
f(х)  В
В  f(х) ограничена.
f(х) ограничена.
§4. Предельный переход в неравенствах.
Теорема 1.
Пусть f(х) имеет стандартную область определения Х, точка хо лежит внутри или является концом одного из промежутков, образующих Х, и пусть 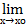 f(х)= L.
f(х)= L.
Если  число В (число А) и если
число В (число А) и если  окрестность (хо
окрестность (хо 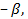 хо+
хо+  ) точки хо такая, что
) точки хо такая, что  х
х  {(хо
{(хо 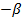 , хо)}
, хо)}  {(хо, хо+
{(хо, хо+  )}
)}  Х: f(х)
Х: f(х)  В (соответственно, f(х)
В (соответственно, f(х)  А), то и L
А), то и L  В (соответственно, L
В (соответственно, L  А).
А).
Следствие.
Если  х
х  Х: А
Х: А  f(х)
f(х)  В и L=
В и L= 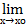 f(х), то А
f(х), то А  L
L  В.
В.
Теорема 2.
Пусть функции f(х), g(х), h(х) имеют стандартную область определения Х, хо лежит внутри или является концом одного из промежутков, образующих Х.
Если  - окрестность (хо
- окрестность (хо 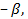 хо+
хо+  ) точки хо (
) точки хо ( >0) такая, что
>0) такая, что  х
х  {(хо
{(хо 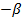 , хо)}
, хо)}  {(хо, хо+
{(хо, хо+  )}
)}  Х: f(х)
Х: f(х)  h(х)
h(х)  g(х) и
g(х) и 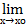 f(х)=
f(х)= 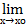 g(х)=L, то
g(х)=L, то  h(х)=L.
h(х)=L.
Теорема 3.
Пусть f1(х) и f2(х) имеют стандартную область определения Х, хо лежит внутри или является концом одного из промежутков, образующих Х, и пусть L1= 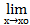 f1(х), L2=
f1(х), L2= 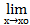 f2(х), и
f2(х), и  - окрестность точки хо (хо
- окрестность точки хо (хо 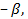 хо+
хо+  ) такая, что
) такая, что  х
х  {(хо
{(хо 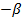 , хо)}
, хо)}  {(хо, хо+
{(хо, хо+  )}
)}  Х: f1(х)
Х: f1(х)  f2(х), то L1
f2(х), то L1  L2.
L2.
Теоремы 1, 2, 3 доказываются применением теорем главы 2 о предельном переходе в неравенствах для последовательностей значений заданных функций.
Докажем теорему 2.
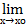 f(х)=
f(х)= 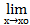 g(х)=L.
g(х)=L.
Возьмём произвольную последовательность {хn} типа Гейне 
 n: хn
n: хn  Х,
Х,  n: хn
n: хn  хо,
хо,  хn= хо.
хn= хо.
Так как  хn= хо
хn= хо 
 >0
>0  о
о  n>
n>  о: │хn - хо│<
о: │хn - хо│< 

 n>
n>  о: хn
о: хn  (хо
(хо 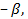 хо+
хо+  ) и, следовательно, по условию f(хn)
) и, следовательно, по условию f(хn)  h(хn)
h(хn)  g(хn).
g(хn).
А так как  f(хn)=
f(хn)= 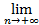 g(хn)=L
g(хn)=L 
 h(хn)=L (по теореме о „жулике”).
h(хn)=L (по теореме о „жулике”).
Последовательность {хn} типа Гейне была выбрана произвольной, то по определению предела функции в точке в смысле Гейне 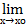 h(х)=L.
h(х)=L.
§5. Односторонние пределы функции в точке. (пределы слева и справа)
Определение.
Пусть функция f(х) имеет стандартную область определения Х, точка хо лежит внутри или является правым (левым) концом одного из промежутков, образующих Х.
Говорят, что f(х) имеет в точке хо предел слева (справа) равный L и пишут  f(х)=L (соответственно,
f(х)=L (соответственно,  f(х)=L), если
f(х)=L), если
(Г)1  {хn}
{хn} 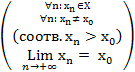 : (К)1
: (К)1  0
0  >0
>0  х
х
(х  Х, хn<хо (соотв. хn>хо), │x - хо│<
Х, хn<хо (соотв. хn>хо), │x - хо│<  ):
):
 f(хn)=L │f(х)- L│<
f(хn)=L │f(х)- L│< 
Так же, как и для обычных пределов (Г)1 и (К)1 эквивалентны.
Односторонние пределы обладают такими же простейшими арифметическими свойствами - свойствами, связанными с неравенствами, что и обычные пределы (во всех случаях в доказательстве надо заменит хn  хо неравенствами хn< хо (хn>хо) или х< хо (соответственно х>хо)
хо неравенствами хn< хо (хn>хо) или х< хо (соответственно х>хо)
Теорема.
Пусть f(х) имеет стандартную область определения Х и точка хо лежит внутри или является концом одновременно двух смежных промежутков из Х, и пусть в точке хо f(х) имеет равные односторонние пределы:  f(х)=
f(х)=  f(х)=L (1).
f(х)=L (1).
Тогда в точке хо f(х) имеет предел, и он равен L.
Дата добавления: 2015-10-30; просмотров: 149 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Докажем теорему 2. | | | Доказательство. |