
|
Читайте также: |
Докажем основной случай.
Пусть {xn} неограниченна сверху и возрастает.
{xn} неограниченна сверху 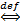
 E>0
E>0 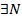 : xN>E.
: xN>E.
А так как {xn} возрастает, то 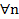 : xn
: xn  xn+1
xn+1  x1
x1  x2
x2  …
…  xN
xN  xN+1
xN+1  …
…  xn
xn  … при n>N
… при n>N 
 E>0
E>0  N
N  n>N: xn>E
n>N: xn>E  {xn} стремится к +
{xn} стремится к +  .
.
Задача.
Доказать самостоятельно, что любая неограниченная снизу убывающая последовательность стремится к -  .
.
§6. Частичные последовательности (подпоследовательности).
Пусть задана числовая последовательность { xn} 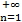 ={x1, x2, …, xn, …} (1)
={x1, x2, …, xn, …} (1)
Тогда можно образовать следующие последовательности:
{x1, x3, x5, …, x2k-1, …} nk=2k-1, k=1, 2, …
{x2, x4, …, x2k, …} nk=2k, k=1, 2, …
{x1, x4, x9, …, xk·k, …} nk= k2, k=1, 2, …
{x2, x3, x5, x6, …, xpk, …} nk=pk, k=1, 2, …
Определение.
Частичной последовательностью или подпоследовательностью последовательности (1)называется любая последовательность вида
{xn1, xn2, …, xnk, …}, в которой номера n1<n2<…<nk<… образуют строго возрастающую последовательность, при этом nk  k, k=1, 2, …
k, k=1, 2, …
Теорема 1.
Любая подпоследовательностьсходящейся последовательности сходится и имеет тот же предел.
Доказательство.
Пусть {xn} сходится 
 а
а  0
0  N
N  n>N: │xn-а│<
n>N: │xn-а│<  и пусть { xn}
и пусть { xn} 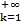 - произвольная подпоследовательность последовательности {xn}.
- произвольная подпоследовательность последовательности {xn}.
Докажем, что  xn=а.
xn=а.
Так как {nk} строго возрастает и  : nk
: nk  k, то по теореме §5 {nk} стремится к +
k, то по теореме §5 {nk} стремится к + 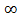

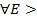 0, а значит и для E=N>0
0, а значит и для E=N>0  номер K такой, что
номер K такой, что  k>K: nk>N
k>K: nk>N 
 >0
>0 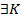
 >K: │xn-а│<
>K: │xn-а│< 
 а=
а=  xnk.
xnk.
Теорема 2.
Любая подпоследовательность последовательности стремящейся к +  (-
(-  (соответственно, к -
(соответственно, к -  ).
).
Доказательство.
Пусть {xn} стремится к + 
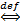
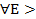 0
0  N
N  n>N: xn>E.
n>N: xn>E.
Пусть {xnk} – произвольная подпоследовательность последовательности {xn}. Тогда по определению
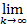 nk=+
nk=+ 

 N>0
N>0 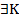
 >K: nk>N
>K: nk>N 
 E>0
E>0 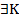
 >K: xnk>E
>K: xnk>E 
 xnk=+
xnk=+  .
.
Задача.
Доказать самостоятельно теорему 2 в случае стремления последовательности к -  .
.
Замечание.
Из сходимости некоторой подпоследовательности сходимостьисходной последовательности, вообще говоря, не вытекает.
Пример 1.
Последовательность {0, 0, …, 0, …} является подпоследовательностью последовательности {0, 1, 0, 2, …}. Она неограниченна.
Пример 2.
Последовательность {1, 0, 1, 0, …} (*) расходится, т.к. она имеет две подпоследовательности {0, 0, …, 0, …} nk=2k, k=1, 2, …,  x2k=0
x2k=0
и {1, 1, …, 1, …} nk=2k-1, k=1, 2, …,  x2k-1=1
x2k-1=1
и предположение о том, что (*) имеет предел приводит к противоречию с теоремой 1.
Возникает вопрос:
Сколько подпоследовательностей (произвольных, но фиксированных) имеет последовательность исходной?
Пусть 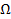 - множество всех подпоследовательностей последовательности.
- множество всех подпоследовательностей последовательности.
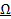 имеет мощность континуума.
имеет мощность континуума.
Определение.
Число  называется частичным пределом {xn}, если
называется частичным пределом {xn}, если  {xnk} – её подпоследовательность такая, что
{xnk} – её подпоследовательность такая, что  xnk=
xnk= 
Рассмотрим множество M всех частичных пределов данной последовательности {xn}.
Возможны следующие варианты:
I. М  .
.
1. М – ограничено 
 inf M и sup M
inf M и sup M
Определение.
Нижним пределом {xn} называется 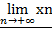 = inf М.
= inf М.
Верхним пределом {xn} называется  = sup М.
= sup М.
2. М –ограниченно снизу и неограниченно сверху.
Тогда по определению 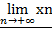 = inf М, а
= inf М, а  =+
=+  .
.
3. М – ограниченно сверху и неограниченно снизу.
Тогда по определению  = sup М, а
= sup М, а 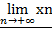 =
=  .
.
II. M= 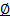 .
.
В этом случае у {xn} нет ни одной сходящейся подпоследовательности.
Например, {1, 2, 3, …, n, …}.
Тогда 1) если у последовательности {xn} существует подпоследовательность, стремящаяся к +  , то
, то  =+
=+  .
.
2) если у последовательности {xn}, существует подпоследовательность, стремящаяся к -  , то
, то 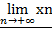 =
=  .
.
§7. Монотонные последовательности.
Теорема.
Любая монотонная ограниченная последовательность сходится.
Дата добавления: 2015-10-30; просмотров: 150 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство. | | | Доказательство. |