Доказательство. Для определённости будем считать, чтоf(x) строго возрастает на X

Для определённости будем считать, чтоf(x) строго возрастает на X, то есть x₁, x₂ X, x₁<x₂: f(x₁)< f(x₂).

Докажем, что f(x) непрерывна на X.

Предположим противное, то есть что x_о X такое, что f(x) терпит разрыв в точке x_о. По теореме 1, точка разрыва x_о является точкой разрыва 1-го рода.

x_о X 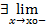f(x)=L₁= sup _X1f(x)

f(x)=L₂= inf _X2 f(x) и L₁ L₂.

Но так как L₁ f(x_о) L₂, то предполагается, что

1) L₁< f(x_о).

Возьмём точку x₁ X₁. Тогда y₁= f(x₁) L₁< f(x_о). y₁= f(x₁)<y_о= f(x_о) (y₁, y_о) 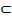Y={y; y=f(x), x X}.

Возьмём произвольную точку y (y₁, y_о) и L₁<y <f(x_о)= y_о.

В самом деле, f(x) строго возрастает x X₁: f(x) L₁<y

x X₂: f(x)> f(x_о)= y_о>y.

Но это невозможно, так как Y={f(x), x X} – промежуток L₁=f(x_о).

2) Пусть f(x_о)< L₂ = f(x)= inf _X2 f(x).

Возьмём некоторое x₂ X₂={x; x>х_о}

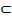y₂=f(x₂) Y весь интервал (y_о, y₂) Y.

Рассмотрим точку y (y_о, y₂) и f(x_о)< y<L₂.

Проверим, что x X: f(x) y. В самом деле, x X₁: f(x)< f(x_о)<y.

x X₂: f(x_о)<y<L₂ f(x).

Но это невозможно, так как Y промежуток.

А тогда f(x_о)= L₂.

И мы получаем L₁= f(x_о)=L₂ f(x)= f(x_о)= f(x) f(x)= f(x_о).

х_о X и f(x)= f(x_о).

Следствие (теоремы 1).

Если функция монотонна на промежутке, и она имеет точки разрыва, то все они точки разрыва 1-го рода.

Следствие (теоремы о промежуточных значениях непрерывной функции и теоремы 2.)

(Критерий непрерывности строго монотонной функции.)

Строго монотонная функция на промежутке X ненулевой длины (в частности, на отрезке [a, b], a<b) является непрерывной на X тогда и только тогда, когда её область значений Y={f(x), x X} является промежутком.

Определение.

Пусть f(x) определена на промежутке X ненулевой длины. Y={f(x), x X} – её область значений.

Функция f(x) называется однозначно обратной на X, если y Y единственное x X такое, что y=f(x).

Определение.

Пусть y=f(x) однозначно обратима на X, Y={f(x), x X} – её область значений.

Функция x=g(y) называется обратной к функции y=f(x), если она определена на Y, и каждому y Y она ставит в соответствие именно то единственной x X, для которого y=f(x).

Обозначение обратной функции: g(y)= f^-1(y), y Y.

Теорема 3.

Любая строго монотонная функция на промежутке X ненулевой длины однозначно обратима на нём.

Дата добавления: 2015-10-30