Классификация точек разрыва функции.

Определение.

Точка разрыва x_о функции f(x) называется точкой разрыва I-го рода, если

(А). x_о X и x_о лежит внутри одного из промежутков, образующих X, и в точке x_о существуют односторонние пределы функции f(x), то есть 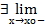f(x) и 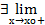f(x).

y

x

x

y

 

(В). x_о X и является концом только одного промежутка из X, и в точке x_о существует соответствующий единственные односторонний предел функции и он не равен значению f(x_о).

(С). x_о 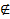X, но является концом одновременно двух смежных промежутков из X и в точке x_о 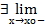f(x) и 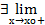f(x).

y

x

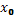
x

y

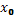
Определение.

Точка разрыва I-го рода называется точкой устранимого разрыва, если 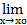f(x).

Слово устранимый означает, что можно взять такую функцию g(x), которая всюду совпадает с f(x), кроме точки x_о, и g(x) непрерывна в точке x_о.

Определение.

Любая точка разрыва, не являющаяся точкой разрыва I-го рода, называется точкой разрыва II-го рода.

Примеры.

1. f(x)= , (– , 0) (0, + )

f(x)=+ , 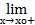f(x)=+

y

x

2. f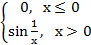(x)= X=(, + )

y

x

-1

-1

Точка x_о=0 является точкой разрыва II-го рода.

Определение.

Говорят, что функция f(x) со стандартной областью определения X непрерывна справа (слева) в точке x_о, если

(1) x_о X

(2) 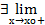f(x) (соотв. 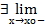f(x))

(3) 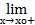f(x)= f(x_о) (соотв. f(x)= f(x_о))

Простейшие свойства непрерывных функций.

Теорема 1. (Об арифметических свойствах непрерывных функций.)

Пусть функции f₁(x) и f₂(x) имеют общую стандартную область определения X, и обе эти функции непрерывны в точке x_о.

Тогда в точке x_о непрерывны и функции:

1. f₁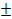(x) f₂(x)

2. f₁(x)· f₂(x)

3. Если f₂(x_о) 0, то в точке x_о непрерывна и функция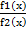

Доказательство.

Докажем теорему 1 для функции f₁(x) 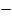f₂(x).

Функция f₁(x) определена на X₁, f₂(x) определена на X₂ и X=X₁ X₂.

Для функции f₁(x) 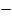f₂(x) проверим выполнение всех трёх условий непрерывности функции в точке x_о.

(1). x_о X.

f₁(x), f₂(x) непрерывны в точке x_о x_о X₁, x_о X₂ x_о X.

(2).

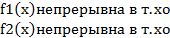
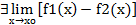
согласно арифметическим свойствам предела функции.

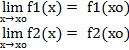
(3). 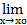(f₁(x) 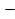f₂(x))= f₁(x_о) 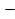f₂(x_о)

Все три условия выполнены, следовательно, функция f₁(x) 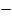f₂(x) непрерывна в точке x_о.

Определение.

Пусть f(z) имеет стандартную область определения Z, функция (x) имеет стандартную область определения X, и пусть x X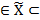: (x) Z.

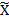Тогда функция F(x)=f( (x)), определённая на , называется сложной функцией или суперпозицией функций z= (x) и y=f(z).

Теорема 2. (О непрерывности сложной функции.)

Пусть функции f(z), (x) и F(x) имеют стандартные области определения Z, X и 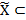X соответственно, и пусть f(z) непрерывна в точке z_о Z, z_о= (x_о), (x) непрерывна в точке x_о. Тогда F(x) непрерывна в точке x_о.

Дата добавления: 2015-10-30