
|
Читайте также: |
Докажем, что 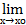 f(х)=L.
f(х)=L.
Из (1) следует, что  0
0 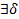 1>0
1>0  х (х
х (х  Х, х< х о, │x - хо│<
Х, х< х о, │x - хо│<  1): │f(х)- L│<
1): │f(х)- L│<  (2).
(2).
Из (1) следует, что  0
0 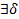 2>0
2>0  х (х
х (х  Х, х>х о, │x - хо│<
Х, х>х о, │x - хо│<  2): │f(х)- L│<
2): │f(х)- L│<  (3).
(3).
Возьмём произвольное  0 и зафиксируем его.
0 и зафиксируем его.
Положим  =min{
=min{  1,
1,  2}>0.
2}>0.
Тогда  х (х
х (х  Х, х
Х, х 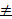 х о, │x - хо│<
х о, │x - хо│<  ): │f(х)- L│<
): │f(х)- L│<  , так как х
, так как х  хо, то либо х< хо и тогда справедливо (2), либо х>хо и тогда справедливо (3).
хо, то либо х< хо и тогда справедливо (2), либо х>хо и тогда справедливо (3).
§6. Пределы функций на бесконечности.
Примеры.
1. y= f(х)= arctg( x ), Х=( , +
, +  ).
).
При х  y
y  , при х
, при х  +
+  y
y 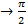 .
.
2. y= f(х)=  , Х=(
, Х=( , +
, +  ). y
). y  0 при х
0 при х  .
.
О таких функциях в этом параграфе и пойдёт разговор.
Определение.
Пусть f(х) имеет стандартную область определения Х, и пусть множество Х неограниченно сверху (Х неограниченно снизу).
Говорят, что число L является пределом функции f(х) при х  +
+  (соответственно, при х
(соответственно, при х  ) и пишут
) и пишут  f(х)=L (соответственно,
f(х)=L (соответственно, 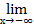 f(х)=L), если
f(х)=L), если
(Г)2 (К)2
 {хn}
{хn}  :
:  0
0  D>0
D>0  х (х
х (х  Х, х>D):
Х, х>D):
│f(х)- L│< 
 f(хn)=L (соотв. х<D): │f(х)- L│<
f(хn)=L (соотв. х<D): │f(х)- L│< 
Определения (Г)2 и (К)2 эквивалентны.
(Г)2 и (К)2 обладают всеми свойствами пределов функций, арифметическими и другими.
Замечание.
Неограниченная сверху область определения Х функции f(х) может содержать промежуток [a, +  ) или (a, +
) или (a, +  ), но необязательно, а неограниченная снизу область определения Х функции f(х) - промежутки (
), но необязательно, а неограниченная снизу область определения Х функции f(х) - промежутки ( , b] или (
, b] или ( b), и тоже необязательно.
b), и тоже необязательно.
Например.
1. f(х)=  , Х=(
, Х=( , 0)
, 0)  (0, +
(0, +  ).
).
2. f(х)=  , Х=
, Х=  ,
, 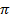 (n+1))
(n+1))
§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
1. f(х)= 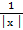 , Х=(
, Х=( , 0)
, 0)  (0, +
(0, +  ). При х
). При х  0 f(х)
0 f(х)  +
+ 
2. f(х)=х3, Х=(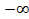 , +
, +  ). При х
). При х  f(х)
f(х)  , при х
, при х  +
+  f(х)
f(х)  +
+  .
.
Определение.
Пусть f(х) имеет стандартную область определения Х, точка хо лежит внутри или является концом одного из промежутков, образующих Х.
Говорят, что f(х) стремится к +  (к
(к  ) при х
) при х  хо и пишут
хо и пишут 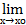 f(х)= +
f(х)= +  (соответственно,
(соответственно, 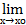 f(х)=
f(х)= 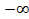 ), если
), если
(Г)3 (К)3
 {хn}
{хn} 
 Е>0
Е>0 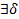 >0
>0  х (х
х (х  Х, х
Х, х  хо, │x - хо│<
хо, │x - хо│<  ):
):
f(х)>Е (соотв. f(х)< 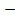 Е)
Е)
 f(хn)= +
f(хn)= + 
(соотв.  f(хn)=
f(хn)= 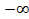 )
)
Определения (Г)3 и (К)3 эквивалентны. (Г)3 и (К)3 обладают всеми свойствами пределов функций.
Аналогично определяются:
 f(х)= +
f(х)= + 
 f(х)= +
f(х)= + 
 f(х)=
f(х)= 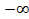
 f(х)=
f(х)= 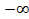
Замечание.
Иногда рассматривают функцию f(х), стремящуюся к  при х
при х  +
+  , при х
, при х  , и стремящуюся к +
, и стремящуюся к +  и к
и к  на бесконечности.
на бесконечности.
Например.
Пусть f(х) имеет стандартную область определения Х, Х –неограниченно снизу, тогда 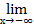 f(х)= +
f(х)= +  определяется так:
определяется так:
(Г)4 (К)4
 {хn}
{хn}  :
:  Е>0
Е>0  D>0
D>0  х (х
х (х  Х, х<
Х, х< 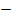 D):
D):
 f(хn)= +
f(хn)= + 
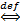 f(х)>Е
f(х)>Е
 Е>0
Е>0 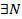
 n>N: f(хn)>Е
n>N: f(хn)>Е
§8. Сравнение бесконечно малых и бесконечно больших функций.
I. Определение.
Пусть  (х) имеет стандартную область определения Х и точка хо лежит внутри или является концом одного из промежутков, образующих Х.
(х) имеет стандартную область определения Х и точка хо лежит внутри или является концом одного из промежутков, образующих Х.
Функция  (х) называется бесконечно малой при х
(х) называется бесконечно малой при х  хо, если
хо, если 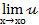 (х)=0.
(х)=0.
Определение.
Пусть  (х) и
(х) и  (х) имеют общую стандартную область определения Х, и обе являются бесконечно малыми при х
(х) имеют общую стандартную область определения Х, и обе являются бесконечно малыми при х  хо.
хо.
Говорят, что б.м.  (х) и
(х) и  (х) при х
(х) при х  хо имеют один и тот же порядок малости и пишут
хо имеют один и тот же порядок малости и пишут  (х)=
(х)=  x
x  xo[
xo[  (х)], если
(х)], если  =L
=L  0.
0.
Замечание.
Мы в данном случае предполагаем, что отношение 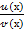 определено на Х
определено на Х  (хо-h, хо+h), h>0, то есть
(хо-h, хо+h), h>0, то есть  (х)
(х)  0 несмотря на то, что
0 несмотря на то, что  (х)=0.
(х)=0.
Определение.
Говорят, что две б.м.  (х) и
(х) и  (х) при х
(х) при х  хо эквивалентны, если
хо эквивалентны, если  =1.
=1.
Определение.
Говорят, что б.м.  (х) при х
(х) при х  хо имеет более высокий порядок малости относительно б.м.
хо имеет более высокий порядок малости относительно б.м.  (х) при х
(х) при х  хо, если
хо, если  =0 и пишут
=0 и пишут  (х)=
(х)= 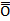 х
х  хо[
хо[  (х)].
(х)].
Определение.
Говорят, что б.м.  (х) при х
(х) при х  хо имеет порядок малости равный р относительно б.м.
хо имеет порядок малости равный р относительно б.м.  (х) при х
(х) при х  хо, если
хо, если  =L
=L  0 и пишут
0 и пишут  (х)=
(х)=  x
x  xo[
xo[  р(х)].
р(х)].
Определение.
Если не существует  , и функция
, и функция  при х
при х  хо, то говорят, что б.м.
хо, то говорят, что б.м.  (х) и
(х) и  (х) при х
(х) при х  хо несоизмеримы.
хо несоизмеримы.
Примеры.
1.  (х)=х и
(х)=х и  (х)=│x│ при х
(х)=│x│ при х  0 несоизмеримы.
0 несоизмеримы.
2.  (х) и │
(х) и │  (х)│ - б.м., при х
(х)│ - б.м., при х  хо несоизмеримы.
хо несоизмеримы.
3. f(х)=х и g(х)=х·  - б.м. при х
- б.м. при х  0
0  g(х)=
g(х)=  x
x  0[
0[ 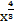 ]
]  р=
р= 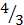 – порядок малости при х
– порядок малости при х  0 относительно х.
0 относительно х.
II. Бесконечно большие –б.б.
Пусть  (х) и
(х) и  (х) – бесконечно большие функции при х
(х) – бесконечно большие функции при х  хо.
хо.
Определение.
Говорят, что б.б.  (х) и
(х) и  (х) имеют один и тот же порядок роста при х
(х) имеют один и тот же порядок роста при х  хо и пишут
хо и пишут  (х)=
(х)=  x
x  xo[
xo[  (х)], если
(х)], если 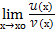 =L
=L  0.
0.
Определение.
Говорят, что б.б.  (х) имеет порядок роста равный р относительно
(х) имеет порядок роста равный р относительно  (х) при х
(х) при х  хо, если
хо, если 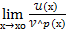 =L
=L  0 и пишут
0 и пишут  (х)=
(х)=  x
x  xo[
xo[  р(х)].
р(х)].
Определение.
Говорят, что б.б.  (х) более высокого порядка роста относительно б.б.
(х) более высокого порядка роста относительно б.б.  (х) при х
(х) при х  хо, если
хо, если 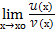 =
=  .
.
§9. Специальные пределы функций.
I. 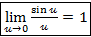
Функция f( )=
)=  определена на Х=(
определена на Х=( , 0)
, 0)  (0, +
(0, +  ), точка
), точка  о=0 является концом одновременно двух смежных промежутков из Х. так как рассматриваем
о=0 является концом одновременно двух смежных промежутков из Х. так как рассматриваем  , то достаточно рассмотреть этот предел для сужения нашей функции f(
, то достаточно рассмотреть этот предел для сужения нашей функции f( ), то есть для функции
), то есть для функции  ,
,  (
( , 0)
, 0)  (0,
(0,  ).
).
Рассмотрим каждый интервал отдельно.
1. 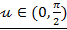

 >0, tg
>0, tg  >0.
>0.
| u |
| y |
| 0 C 1 u |
| D B |
Вычислим площадь треугольника  А0В, сектора
А0В, сектора  и △А0D.
и △А0D.
 А0В
А0В  △А0D.
△А0D.
пл.  А0В<пл.
А0В<пл. 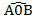 <пл. △А0D.
<пл. △А0D.
Из элементарной геометрии:  ·1·
·1·  <
<  ·1·
·1·  <
<  ·1· tg
·1· tg 
 <
<  < tg
< tg  и т.к.
и т.к.  >0, то 1<
>0, то 1< 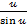 <
< 

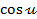 <
<  <1.
<1.
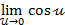 =
=  =1
=1
Тогда по теореме о предельном переходе в неравенствах для трёх функций  =1
=1
2. 

 <
<  <0
<0  0<(
0<( )<
)< 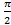

 <
< 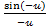 <1.
<1.
Согласно чётности 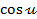 и нечётности
и нечётности  :
: 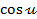 <
<  <1.
<1.
 =1
=1  =
=  =1
=1  согласно теореме §5 получаем
согласно теореме §5 получаем
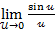 =1.
=1.
II. 
Рассмотрим g(х)=  ; Х=(
; Х=( ,
, 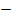 1)
1)  (0, +
(0, +  )
)  стандарстная область определения функции g(х).
стандарстная область определения функции g(х).
Докажем, что 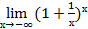 =
=  =e.
=e.
Для этого сначала докажем, что 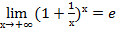

 >0
>0  D>0
D>0  х (х
х (х  Х, х>D): │
Х, х>D): │ 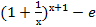 │<
│<  .
.
А так как g(х)=  , то
, то  =
=  =e
=e
1. Возьмём произвольное  >0 и зафиксируем его. Ищем D>0.
>0 и зафиксируем его. Ищем D>0.
 =e
=e 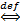
 >0, а значит и для нашего фиксированного
>0, а значит и для нашего фиксированного  >0
>0  N1
N1  n> N1: │
n> N1: │  e│<
e│<  .
.
e  <
< 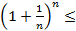 e= sup {
e= sup {  } (*)
} (*)
А так как 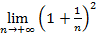 =1
=1  >0,
>0,  >0,
>0,  N2
N2  n>N2: │
n>N2: │  │<
│<  1
1 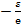 <
< 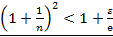
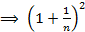 <1+
<1+  (**)
(**)
Положим N=max{N1, N2}, D=N+1>0.
Тогда  х>D и
х>D и  =n получаем n
=n получаем n  х<n+1
х<n+1  n>N
n>N  N1 и n>N
N1 и n>N  N2
N2
e  <
< 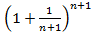 <
<  <
< 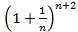 =
=  e(1+
e(1+  )=e+
)=e+ 

2. Докажем, что │ 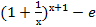 │<
│< 
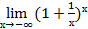 =e.
=e.
Используем определение (Г)2.
Возьмём произвольную последовательность {xn} типа Гейне ( n: хn
n: хn  Х
Х  хn=
хn=  ) и проверим, что
) и проверим, что  g(х)=e.
g(х)=e.
Так как Х=( ,
,  1)
1)  (0, +
(0, +  ), то не ограничивая общности можно считать, что
), то не ограничивая общности можно считать, что  n: xn<
n: xn<  1<0, то есть xn
1<0, то есть xn  (
( ,
, 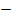 1). Рассмотрим последовательность {xn’}, где
1). Рассмотрим последовательность {xn’}, где  n: xn’=
n: xn’= 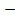 xn>1>0
xn>1>0  xn’=+
xn’=+  .
.
 n: g(xn)=
n: g(xn)=  =
=  =
=  =
=  =
= 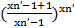 =
=  =
= 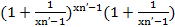 =g(xn’
=g(xn’ 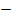 1)
1) 
В силу выбора последовательности {xn}, последовательность {xn 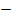 1} обладает свойствами:
1} обладает свойствами:
1.  n: xn’
n: xn’ 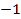 =
= 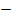 xn
xn  1
1  (0, +
(0, +  )
)  Х
Х
2.  (xn’
(xn’  1)=+
1)=+  (ибо
(ибо  хn=
хn=  )
)
А тогда по доказанному в п.1  g(хn)=
g(хn)= 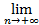 g(xn’
g(xn’ 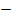 1)
1)  =e.
=e.
А так как последовательность была выбрана произвольно, то  g(хn)
g(хn)  .
.
III. h(z)= 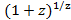 , Z==(
, Z==(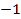 , 0)
, 0)  (0, +
(0, +  ).
).
Докажем, что  h(z)=
h(z)= 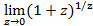 =e.
=e.
Для этого докажем, что  h(z)=
h(z)=  h(z)=e.
h(z)=e.
Замечание.
Справедливы следующие утверждения.
Докажите их самостоятельно.
Дата добавления: 2015-10-30; просмотров: 160 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство. | | | Утверждение 1. |