Доказательство. Тогда последовательность { }: 1) имеет смысл

I. Пусть y_n=b, b .

Тогда последовательность { 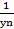}: 1) имеет смысл

2) сходится

3) её предел равен

1) { 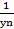} имеет смысл, то есть существует номер n_о такой, что для любого n _о: y_n , то есть { 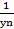} определена.

В самом деле, т.к. y_n=b 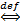для каждого 0, а значит и для >0, существует номер N такой, что для любого номера n>N

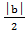│y_n-b│< b- <y_n<b+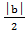

Пусть b>0. │b│=b.

Тогда 0<b- ∙b= <y_n< ∙b (*)

Пусть b<0. │b│= - b.

Тогда ∙b< y_n< ∙b<0 (**).

Тогда для любого n N+1: y_n и { 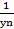} опеределена.

2) Покажем, что { 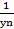} ограничена.

Для любого n>N: либо 0< <y_n │ │< ,

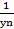либо y_n< <0 │ │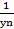< { 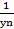} ограничена.

3) Докажем, что { 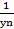} сходится и её предел равен .

Так как y_n=b для любого n: y_n=b+ _n, где { _n} – б.м.

Пусть n _о: = = (b - y_n) = _n.

{ _n } по лемме 3 §2 б.м., ибо {b- y_n }={- _n } – б.м.

А тогда 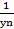= + - = + _n, { _n } б.м. и согласно теореме 1§2, = .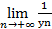

II. Докажем теперь, что{x_n∙ }= { } 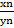сходится.

x_n=а, = .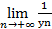

Тогда по теореме 3 { 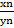} сходится и её предел равен .

Теорема 6.

Пусть {x_n} сходится и x_n=а.

Тогда {│x_n│} сходится и │x_n│=│а│.

Доказательство.

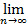x_n=а для каждого >0 существует номер N такой, что для любого номера n>N: │x_n - а│< .

Возьмём произвольное >0, фиксируем его. Тогда

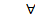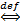
n>N: ││x_n│ - │а││ │x_n - а│< │x_n│=│а│.

Глава 3.Некоторые сведения из математической логики.

§1. Предложение.

(1) Волга впадает в Балтийское море.

(2) 117<121

(3) x отец y

(4) =i<3

(5) z исполнилось 17 лет

(6) 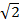- рациональное число

(7) красного цвета

Определение.

Предложением называется высказывание, которое может быть истинным или ложным.

(1), (2), (3), (5), (6) – предложения. (часть из них истинны – (2), (3), (5); (1), (6) – ложны)

(4) и (7) не являются предложениями, так как они оба полностью бессмысленны, что не могут быть ни истинными, ни ложными, то есть лишены содержания.

Условимся обозначать предложения большими латинскими буквами А, В, С, ….

Вместе с каждым предложением А возникает предложение Ā - „не А”.

По определению считается, что Ā ложно (истинно) тогда, когда А истинно (ложно).

(1). Закон противоречия.

Ни при каком предложении А не могут быть А и Ā. Либо оба истинны, либо ложны.

(3) Закон исключения третьего.

Для всякого предложения А оно само или его отрицание Ā истинно.

С точки зрения математической логики каждый закон физики и всякая теорема математики являются предложениями.

Над предложениями могут производится некоторые действия (операции).

Пусть задана упорядоченная пара предложений А и В.

Сложение.

Суммой или дизъюнкцией предложений А и В называется такое новое предложение, обозначаемое А В, которое читается „А или В”, причём А В истинно, если истинно хотя бы одно из предложений А или В.

Умножение.

Определение.

Произведение или конъюнкцией двух предложений называется такое новое предложение, которое обозначается А В и читается „А и В”, причём А В истинно, когда каждое из предложений и А и Вистинны.

Импликация.

Определение.

Импликацией предложений А и В называется такое новое предложение, обозначаемое А В, которое читается следующим образом „из А следует В”, или „если А то В”.

Причём предложение А В истинно во всех случаях, кроме одного, когда А – истинно, а В – ложно

Пример.

А: n – кратно 4

В: n – чётно

Тогда А 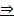В.

Эти введённые символы позволяют записать законы логики в простом виде:

(1) А Ā – ложно при любом А.

(2) А Ā – истинно при любом А.

Импликация в обе стороны, т.е. символ означает - равносильно.

Для любых А, В, С:

(3) А (А В) (А С)

(4) А (В С) (А В) (А С)

(4) И (4) – распределительные законы.

Дата добавления: 2015-10-30