Доказательство. Пусть f(x) определена на [a, b], a<b

Пусть f(x) определена на [a, b], a<b. f(x) непрерывна на [a, b].

1. Докажем, что f(x) ограничена на [a, b] сверху М x [a, b]: f(x) М.

Предположим, что это не так, то есть М x´ [a, b]: f(x´)>М.

Тогда для М=1 x₁´ [a, b]: f(x₁´)>1

для М=2 x₂´ [a, b]: f(x₂´)>2

……………………………….

для М=n x_n´ [a, b]: f(x_n´)>n

……………………………….

Мы построили последовательность {x_n´} такую, что n: x_n´ [a, b], и {f(x_n´)} такова, что f(x_n´)=+ .

Проверим, что {f(x_n´)} стремится к + .

f(x_n´)=+ E>0 N n>N: f(x_n´)>E.

Возьмём произвольное E>0 и зафиксируем его. Тогда по аксиоме Архимеда N – натуральное число такое, что N>E.

Тогда n>N: f(x_n´)>n>N>E n>N: f(x_n´)>E.

А так как n: x_n´ [a, b], то {x_n´} ограничена, а тогда по теореме Больцано-Вейерштрасса у неё существует сходящаяся подпоследовательность {x_nk´}.

Пусть x_nk´=с, а так как k: a x_nk´ b, то по теореме о предельном переходе в неравенствах для одной последовательности получаем a с b с [a, b].

Но по условию теоремы f(x) непрерывна на [a, b], следовательно, и в точке с f(x_n´)= f(с) и мы пришли к противоречию, так как любая подпоследовательность последовательности, стремящейся к + , стремится к +

2. Пусть f(x) непрерывна на [a, b].

Докажем, что f(x) ограничена на [a, b] снизу 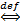m x [a, b]: m f(x).

Рассмотрим функцию g(x)= –f(x). По арифметическим свойствам непрерывной функции, g(x) непрерывна на [a, b] и по доказанному в п.1, g(x) ограничена сверху на [a, b], то есть М x [a, b]: g(x) M, ибо g(x)= –f(x) M f(x) –M=m x [a, b]: f(x) m.

Следовательно, f(x) ограничена на [a, b] и сверху и снизу f(x) ограничена на [a, b].

Замечание 1.

Теорема 2 не распространяется на функции, непрерывные на промежутках другого вида.

Примеры.

1. f(x)= , X=(0, 1). f(x) непрерывна на (0, 1), но не ограничена на интервале (0, 1) сверху.

2. f(x)=x², X=(– , + ). f(x) непрерывна на (– , + ), но не ограничена на (– , + ) сверху.

Замечание 2.

Если f(x) имеет стандартную область определения X и непрерывна на X, то теорема 2 применяется к сужению непрерывной функции f(x) на любом отрезке [a, b] 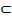X, и эта функция сужения на [a, b] ограничена на [a, b].

Теорема 3. (Вторая теорема Вейерштрасса о достижении функцией, непрерывной на отрезке, своих точных граней.)

Любая функция, непрерывная на отрезке, достигает на нём своих точных, верхней и нижней, граней.

Дата добавления: 2015-10-30