
Читайте также:
|
Если последовательность {yn} такова, что  yn=+
yn=+  , то последовательность {
, то последовательность { 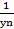 }имеет смысл, и она бесконечно малая, то есть
}имеет смысл, и она бесконечно малая, то есть 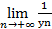 =0.
=0.
Утверждение 2.
Если последовательность{yn} такова, что  n: yn>0 (
n: yn>0 ( n: yn<0) и
n: yn<0) и  yn=0, то {
yn=0, то { 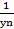 } бесконечно большая, то есть
} бесконечно большая, то есть  (соответственно,
(соответственно, 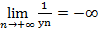 )
)
Вернёмся к функции h(z).
Надо доказать, что  h(z)=e,
h(z)=e, 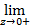 h(z)=e.
h(z)=e.
Возьмём произвольную последовательность {zn} такую, что  n: zn>0 и
n: zn>0 и  n: хn=
n: хn=  и
и  zn=0
zn=0 
 хn=+
хn=+  .
.
Рассмотрим последовательность соответствующих значений функции h(z): {h(z)}= {  }={
}={ 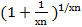 }={g(хn)}.
}={g(хn)}.
Но, следовательно,  h(zn)=
h(zn)= 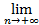 g(хn)=e
g(хn)=e 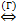
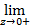 h(z)=e.
h(z)=e.
Аналогично доказывается, что  h(z)=e.
h(z)=e.
А тогда из равенства 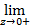 h(z)=
h(z)=  h(z)=e по теореме §5 следует, что
h(z)=e по теореме §5 следует, что  =e.
=e.
Глава 4. Непрерывность функции.
Определение непрерывной функции.
Примеры.
1. f(x)=x2+1,
X=( , +
, +  )
)
| y |
| x |
2. f(x) = 
X=(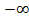 , +
, + 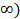
| y |
| x |
3. f(x)=x2+1,
X=(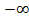 , 0
, 0  0, +
0, +  )
)
| y |
| x |
4. f(x)= 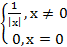
X=(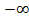 , +
, + 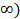
| y |
| x |
5. f(x)= 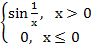
X=(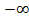 , +
, + 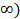
| y |
| x |
| -1 |
| -1 |
Определение.
Говорят, что функция f(x) со стандартной областью определения X непрерывна в точке xо, если
(1) xо  X
X
(2) 
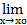 f(x)
f(x)
(3) 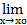 f(x)= f(xо)
f(x)= f(xо)
Расшифровка определения непрерывности функции в точке.
I (1). xо  X, (2) - (3) в смысле Гейне
X, (2) - (3) в смысле Гейне
 {хn}
{хn}  n: хn
n: хn  Х
Х
 хn= хо:
хn= хо:  f(xn) = f(xо)
f(xn) = f(xо)
II (1). xо  X, (2) – (3) в смысле Коши
X, (2) – (3) в смысле Коши
 0
0 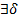 >0
>0  х (х
х (х  Х, │x - хо│<
Х, │x - хо│<  ): │f(х)- f(xо)│<
): │f(х)- f(xо)│< 
III Зафиксируем точку xо  X и возьмём приращение (смещение) △x такое, чтобы xо+△x
X и возьмём приращение (смещение) △x такое, чтобы xо+△x  X. Пусть xо+h= xо+△x=x
X. Пусть xо+h= xо+△x=x  h=△x=x- xо
h=△x=x- xо  = f(xо+h)= f(xо+△x)
= f(xо+h)= f(xо+△x)
(1) xо  X, (2) – (3) означает, что
X, (2) – (3) означает, что
 0
0 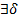 >0
>0  h (xо+h
h (xо+h  Х,
Х,  <
<  ): │f(xо+h) – f(xо) │<
): │f(xо+h) – f(xо) │< 

 f(xо+△x)= f(xо)
f(xо+△x)= f(xо)
IV Зафиксируем xо  X и сместимся из точки xо в точку x= xо+ △x
X и сместимся из точки xо в точку x= xо+ △x  X, не покидая X.
X, не покидая X.
Обозначим через △f=△f(xо; △x)= f(xо+△x) –f(xо) – приращение функции, вызванное смещением △x из точки xо.
(1) xо  X, (2) – (3):
X, (2) – (3): 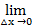 △f (xо; △x)=
△f (xо; △x)=  △f(xо; h)=0.
△f(xо; h)=0.
Определение.
Функция f(x) называется непрерывной на множестве X, если она непрерывна в каждой точке X.
Определение.
Точка xо называется точкой разрыва функции f(x), если
либо xо 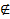 X, но является концом одновременно двух смежных промежутков из X;
X, но является концом одновременно двух смежных промежутков из X;
либо xо  X, но
X, но  f(x);
f(x);
либо xо  X,
X,  f(x), но
f(x), но 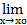 f(x)
f(x)  f(xо).
f(xо).
Определение.
Функция f(x) называется непрерывной, если она не имеет точек разрыва как принадлежащих X, так и не принадлежащих X.
Примеры.
1. f(x)=  , X=(–
, X=(–  , 0)
, 0)  (0, +
(0, +  ).
).
f(x) непрерывна на X, но xо=0 – точка разрыва функции f(x).
2. f(x)=  , X=(0, +
, X=(0, +  )
)
f(x) непрерывна на X и f(x) непрерывная функция.
1) Докажем сначала, что f(x) непрерывна на X.
Возьмём произвольное x  X и дадим ему приращение △x такое, чтобы xо+△x
X и дадим ему приращение △x такое, чтобы xо+△x  X
X  △f(x; △x)=
△f(x; △x)=  –
–  =
=  =
=  Но
Но  при △x
при △x 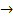 0
0
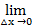 △f(x; △x)=
△f(x; △x)=  0
0  По расшифровке IV
По расшифровке IV  непрерывен в точке x
непрерывен в точке x 
 непрерывен на (0, +
непрерывен на (0, +  )=X.
)=X.
2) Но точек разрыва у  нет, следовательно, f(x)=
нет, следовательно, f(x)=  – непрерывная функция.
– непрерывная функция.
Дата добавления: 2015-10-30; просмотров: 85 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство. | | | Классификация точек разрыва функции. |