
|
Читайте также: |
Так как f(x) и g(x) взаимно обратны, то f(x)  f(xо) и g(y)
f(xо) и g(y)  g(yо) при y=f(x) не обращаются в нуль, если x
g(yо) при y=f(x) не обращаются в нуль, если x  xо, yо= f(xо).
xо, yо= f(xо).
Из непрерывности f(x) в точке xо и g(y) в точке yо следует, что (x 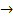 xо)
xо)  (y
(y 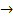 yо).
yо).
Используя теорему о пределе сложной функции и арифметические свойства пределов функции, при ∆x  0, ∆y
0, ∆y  0 получаем
0 получаем  =
=  =
= 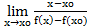 =
=  =
=  .
.
Пример.
f(x)=  , X=
, X=  .
.
X=g(y)=arcsin y, y 
 x
x 
 y=sin x
y=sin x  (
(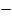 1, 1).
1, 1).
Применяя теорему о производной обратной функции, получаем
(arcsin y)´=  =
=  =
=  =
=  .
.
Таблица производных.
1. f(x)=  , X
, X
Возьмём внутреннюю точку X, сместимся из неё в точку x+∆x, не покидая X, x+∆x  X и пусть ∆x
X и пусть ∆x  0.
0.
По определению f´(x)=  .
.
Пусть x 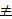 0.
0.
f(x+∆x)  f(x)=
f(x)=  =
=  ·
·  =
=  ·
·  ·∆x
·∆x  f´(x)=
f´(x)= 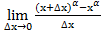 =
=  =
=  ·
·  .
.
 .
.
Пусть x=0,  >1
>1  =∆x.
=∆x.
 =
=  =0
=0


 =1.
=1.
 <0
<0 
 (либо точка x=0 не является внутренней, либо нет производной).
(либо точка x=0 не является внутренней, либо нет производной).
2. f(x)=  , a>0, a
, a>0, a 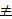 1, X=(
1, X=( , +
, +  )
)
x  X, ∆x
X, ∆x  0, x+∆x
0, x+∆x  X.
X.
а) f(x)= 
 =
=  =
= 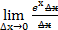 =
=  .
.
б) f(x)=  =
=  .
.
Применяя теорему о производной сложной функции, получаем ( )´=(
)´=( )´=
)´=  .
.

3. f(x)=  , X=(0, +
, X=(0, +  ), x
), x  X, ∆x
X, ∆x  0, x+∆x
0, x+∆x  X.
X.
 =
=  =
=  =
=  .
.

f(x)=  , a>0, a
, a>0, a  1, X=(0, +
1, X=(0, +  ).
).
 =
= 

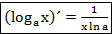
4. f(x)=  , X=(
, X=( , +
, +  ), ∆x
), ∆x  0, x+∆x
0, x+∆x  X.
X.
 =
=  =
=  =
=  =
= 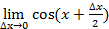 =
=  .
.

5. f(x)=  , X=(
, X=( , +
, +  )
)
 =
=  =
=  =
=  =
=  =
= 

6. f(x)=tg x = 
(tg x)´=  =
=  =
= 

7. f(x) =ctg x =  =
= 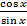

8. y= f(x)=  , X=
, X=  , Y=[
, Y=[ 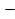 1, 1]
1, 1]
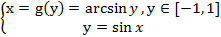
Применяя теорему о производной обратной функции, получаем
(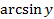 )´=
)´=  =
=  =
=  =
=  , x
, x  (
( ,
,  )
)  y
y  (
(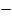 1, 1)
1, 1)

9. x=arcos y =  , y
, y  (
(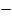 1, 1)
1, 1)

10. x=arctg y, Y=(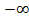 , +
, +  )
)
tg x =y  (arctg y)´=
(arctg y)´=  =
=  =
=  =
= 

11. x=arcctg y, Y=(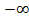 , +
, +  )
)
(arcctg y)´=  =
=  =
=  =
= 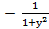

Глава 6. Дифференцируемая функция. Дифференциал.
Понятие дифференцируемой функции в точке и дифференциала.
Определение.
Пусть f(x) имеет стандартную область определения X, xо – внутренняя точка одного из промежутков, образующих X.
Функция f(x) называется дифференцируемой в точке x о, если её приращение в точке xо ∆f(xо; ∆x), вызванное смещением ∆x, может быть представлено в виде ∆f(xо; ∆x)=A·∆x+  (∆x), где A –число, а
(∆x), где A –число, а  (∆x)=
(∆x)=  .
.
Определение.
Пусть f(x) дифференцируема в точке xо. Главная линейная часть приращения функции называется дифференциалом функции f(x) в точке xо.
Обозначение: 

∆f(xо; ∆x)=A·∆x+  (∆x)=df+
(∆x)=df+  , то есть
, то есть  =0
=0
Примеры.
1. f(x)=  , X=(
, X=( , +
, +  )
)
xо=2
∆f(2; ∆x)= 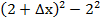 =
=4+4∆x+ 
=4∆x+ 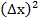
A=4,  (∆x)=
(∆x)=  =
= 
df=4∆x
2. f(x)= 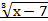 , X=(
, X=( , +
, +  )
)
а) x о =8  ∆f=∆f(8; ∆x)=f(8+∆x)
∆f=∆f(8; ∆x)=f(8+∆x)  f(8)=
f(8)=  =
= 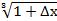
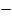 1
1  ∆x
∆x
Главная линейная часть  в точке xо =8.
в точке xо =8.
∆f(8; ∆x)=  ∆x+
∆x+ 
б) xо =7. ∆f(7; ∆x)= ∆f(7; ∆x)  f(7)=
f(7)=  =
=  .
.
Главной частью приращения функции ∆f является  , A=0,
, A=0,  0.
0.
Функция f(x)= 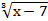 не является дифференцируемой в точке xо=7, так как приращение функции не является линейной от ∆x при
не является дифференцируемой в точке xо=7, так как приращение функции не является линейной от ∆x при 
(∆f(7; ∆x)=  имеет порядок
имеет порядок  при
при  )
)
Теорема 1. (Необходимое условие дифференцируемости функции в точке.)
Пусть f(x) имеет стандартную область определения X, и во внутренней точке xо одного из промежутков X f(x) дифференцируема.
Тогда f(x) непрерывна в точке xо.
Дата добавления: 2015-10-30; просмотров: 131 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство. | | | Особенности кроветворной системы детей различного возраста. Показатели гемограммы. Компоненты свертывающей системы крови. Общеклиническое исследование крови |