Линейные и сопряженные пространства

Пусть - векторное пространство над и

- линейная функция, если .

Ядром функции называется подмножество , на каждом элементе которого функция равна 0: . Ядро – подпространство в . Также если - линейные функции, то и их линейные комбинации с коэффициентами из также линейны.

Сопряженное (дуальное) пространство - множество всех линейных форм (функций).

Теорема. Пусть - конечномерное векторное пространство. Тогда .

Выделим базис в и рассмотрим . Т.е. значение равно символу Кронекера .

1) - линейная функция.

2) 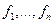- линейно независимы. Пусть и .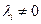
Но 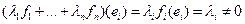. Противоречие.

3) 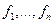- базис. Действительно, рассмотрим произвольную функцию и обозначим Тогда , т.е. .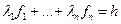

12.02.05

Определение.

Базис { } пространства , такой, что называется дуальным (или сопряжённым) к базису { 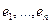} пространства .

Обозначим за пространство, сопряжённое . Тогда, как мы уже знаем, . Мы уже говорили, что два пространства изоморфны, если они имеют равные размерности, но в данном случае, кроме того, можно установить особое соответствие: канонический изоморфизм.

Определение.

Отображение называется каноническим изоморфизмом и задаётся следующим образом: если - это вектор из , то 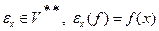. Это и есть определение

Проверим, что отображение --- изоморфизм между и . Для начала --- что линейная функция.

1) Проверим, что , то есть линейная функция из в : , то есть --- действительно линейное отображение из в , что означает, что это отображение задано корректно.

2) Проверим линейность отображения (сначала то, что сумма переходит в сумму). , то есть мы проверили, что . , то есть . Наконец, нужно проверить, биективно ли отображения .

Инъективность. Пусть , где 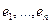--- базис (то есть мы взяли вектор из и разложили его по базису 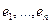). Если --- дуальный базис , то . Так как хотя бы один , то и . То есть . Следовательно, --- инъективное отображение (разные векторы имеют разные образы), потому что для линейного множества достаточно проводить проверку для «0», что мы уже только что проделали.

Сюръективность. Пусть и обозначим . Возьмём . Тогда , то есть . Значит, сюръективно, а из этого следует, что - биекция. Таким образом, --- изоморфизм.

Теорема. Векторы линейно независимы тогда и только тогда, когда 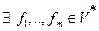, такие что: .

1) Пусть линейно зависимы, то есть существуют коэффициенты 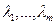(хотя бы один отличен от 0), такие что . Пусть --- столбцы матрицы (*). Тогда для любых линейная комбинация столбцов .

2) Теперь пусть --- линейно независимы. Дополним до базиса : 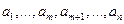и возьмём дуальный базис . Тогда , что и требовалось доказать.

Пусть и --- множество векторов из , таких, что

обращаются в . То есть,

является решением системы линейных уравнений

Теорема. 1) Пусть 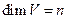. Тогда , где .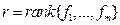

2) Любое подпространство является пространством решений некоторой системы

.

1) Пусть сначала --- линейно независимы. Тогда дополним до базиса в и возьмём дуальный базис 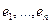в , тогда эти базисы связаны со следующим соотношением: 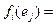. Пусть . Тогда , то есть в этом случае , причём 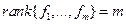. Если же 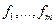линейно зависимы, то существует максимальная линейно независимая подсистема, например, , такая что . Но тогда если , то . То есть (см. выше) отсюда мы уже доказали, что 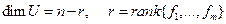, следовательно, 1) доказано.

2) Пусть --- любое подпространство. Выберем базис 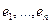в так, что 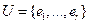. Если --- дуальный базис , то

Следствие 1. Множество решений однородной системы линейных уравнений является подпространством в арифметическом пространстве .

Следствие 2. Любое подпространствo в является пространством решений некоторой однородной системы линейных уравнений.

Пусть – подпространство. По предыдущей теореме существуют ,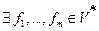

такие, что: .

Если 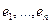--- базис , --- базис (дуальный), то

. Если , то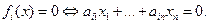

Дата добавления: 2015-10-26